请问:三条边长别离为13,14,15的三角形,其内切圆和外接圆半径是几?
不要慌,各人不要疑惑,我们今天确实想分享一下三角形的面积计算公式,而不是内切圆、外接圆的半径问题。那么为什么要问那个问题呢?
那是因为那个问题和我们今天要讲解三角形面积计算是有慎密联络的。在良多国际数学竞赛中,好比美国数学竞赛(AMC),三角形长短常常见且重要的一类图形,考察十分遍及,那么关于三角形面积公式你晓得几呢?
先看下图:

那里我们枚举了几个计算公式:
(1) A=bh2A=\frac{b h}{2}
二分之一底乘高,那个公式是怎么来的呢?能够用两个一样的三角形拼成一个矩形或者平行四边形,然后除以2就能够了。(2) A=12absinCA=\frac{1}{2} a b \sin C
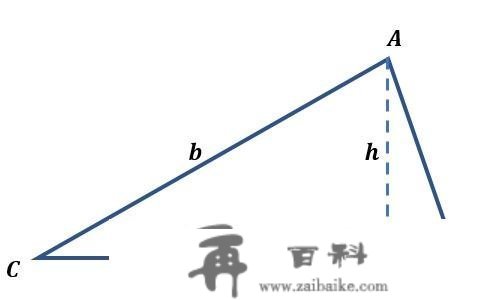 bsinC=hb\sin C=h ,所以仍是二分之一底乘高;
bsinC=hb\sin C=h ,所以仍是二分之一底乘高;(3) A=abc4RA=\frac{a b c}{4 R}
RR 为外接圆半径,那是借助了正弦定理(Law of sine) asinA=bsinB=csinC=2R\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R ,所以 sinC=c2R\sin C=\frac{c}{2R} 带入公式(2)中,就得到了那个公式。讲了外接圆我们看看内切圆。
(4) A=a+b+c2⋅rA=\frac{a+b+c}{2}\cdot r
 保持内切圆圆心与三角形的三个顶点,把 △ABC\triangle ABC
保持内切圆圆心与三角形的三个顶点,把 △ABC\triangle ABC
分红了三个小三角形,那么
S△ABC=S△AOB+S△AOC+S△BOC=12cr+12br+12ar=a+b+c2⋅rS_{\triangle ABC}=S_{\triangle AOB}+S_{\triangle AOC}+S_{\triangle BOC}=\frac{1}{2}cr+\frac{1}{2}br+\frac{1}{2}ar\\=\frac{a+b+c}{2}\cdot r就是我们的半周长乘以内切圆半径。讲到那,我们就想着处理最起头的问题了:
请问:三条边长别离为13,14,15的三角形,其内切圆和外接圆半径是几?
因为内切圆半径、外接圆半径我们都能够通过面积成立等式,所以如今关键点就是要计算出三角形的面积。关于如许一个三角形,似乎我们前面的公式都不是很好用。
那么我们介绍下面的公式(5)海伦公式
 海伦公式证明:
海伦公式证明: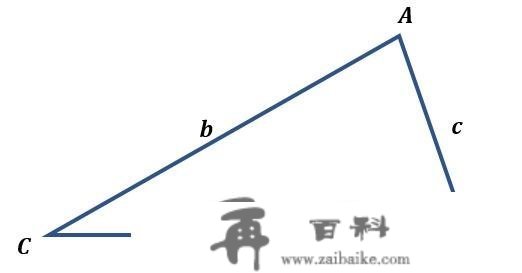 按照余弦定理: cosC=a2+b2−c22ab\cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}
按照余弦定理: cosC=a2+b2−c22ab\cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}
,
三角恒等式: sin2C+cos2C=1⇒sinC=1−cos2C\sin^2C+\cos^2C=1\Rightarrow \sin C=\sqrt{1-\cos^2 C}所以,
sinC=4a2b2−(a2+b2−c2)22ab\sin C=\frac{\sqrt{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}}{2 a b}带入 A=12absinCA=\frac{1}{2}ab \sin C中可知:
A=144a2b2−(a2+b2−c2)2=14(2ab−(a2+b2−c2))(2ab+(a2+b2−c2))=14(c2−(a−b)2)((a+b)2−c2)=(c−(a−b))(c+(a−b))((a+b)−c)((a+b)+c)16=(b+c−a)2(a+c−b)2(a+b−c)2(a+b+c)2=(a+b+c)2(b+c−a)2(a+c−b)2(a+b−c)2=p(p−a)(p−b)(p−c)\begin{aligned} A&=\frac{1}{4} \sqrt{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}\\ &=\frac{1}{4} \sqrt{\left(2 a b-\left(a^{2}+b^{2}-c^{2}\right)\right)\left(2 a b+\left(a^{2}+b^{2}-c^{2}\right)\right)}\\ &=\frac{1}{4} \sqrt{\left(c^{2}-(a-b)^{2}\right)\left((a+b)^{2}-c^{2}\right)}\\ &=\sqrt{\frac{(c-(a-b))(c+(a-b))((a+b)-c)((a+b)+c)}{16}}\\ &=\sqrt{\frac{(b+c-a)}{2} \frac{(a+c-b)}{2} \frac{(a+b-c)}{2} \frac{(a+b+c)}{2}}\\ &=\sqrt{\frac{(a+b+c)}{2} \frac{(b+c-a)}{2} \frac{(a+c-b)}{2} \frac{(a+b-c)}{2}}\\ &=\sqrt{p(p-a)(p-b)(p-c)} \end{aligned}此中, p=a+b+c2p=\frac{a+b+c}{2} 为半周长。 ◻\square有了海伦公式那么肆意三角形的面积我们都可以计算了,好比13-14-15,我们带入公式可知面积为84,所以最起头的问题以13-14-15为三边的三角形的内接圆半径为:
R=abc4S=13×14×154×84=658R=\frac{abc}{4S}=\frac{13\times 14\times 15}{4\times 84}=\frac{65}{8}
内切圆半径为:
r=2Sa+b+c=2×8413+14+15=4r=\frac{2S}{a+b+c}=\frac{2\times 84}{13+14+15}=4 。
其实以13-14-15为三边的三角形是由5-12-13与9-12-15两个曲角三角形拼接而成的。关于肆意的三角形我们若是要计算其内切圆半径、外接圆半径,我们就能够通过海伦公式 S=p(p−a)(p−b)(p−c)S=\sqrt{p(p-a)(p-b)(p-c)} 先得到其面积,然后再借助公式 R=abc4SR=\frac{a b c}{4 S} 、 r=2Sa+b+cr=\frac{2 S}{a+b+c} 得到其内切圆半径或外接圆半径。
当然三角形的面积计算公式还有(6) A=12klA=\frac{1}{2}kl
 能够拆成两个同底不等高的三角形面积之和。
能够拆成两个同底不等高的三角形面积之和。当晓得三角形三个顶点的坐标时,我们也能够用(7)Shoelace Theorem

关于定理的证明详见《肆意多边形面积计算公式》
若是再特殊一点,三角形的顶点都在格点上,我们还能够用(8)Picks Theorem

总结:
那里我们介绍了良多种三角形面积的计算公式,在竞赛中我们就按照标题问题所给的前提选择适宜的公式停止计算,有时候我们会有简单的办法计算,再不济我们还有海伦公式,好比2019-AMC12B-18:

当然,学了那么多三角形的面积计算公式仍是要灵敏应用,好比计算外接圆半径与内切圆半径时,我们都是通过三角形面积做为中间桥梁得到的。
不晓得关于三角形面积各人还有什么设法,欢送交换沟通~~
想领会肆意四边形或多边形面积公式的可看下列文章:
双木行月Tong:【国际数学竞赛】四边形面积公式知几?587 附和 · 44 评论文章 双木行月Tong:【国际数学竞赛】肆意多边形面积计算公式870 附和 · 46 评论文章
双木行月Tong:【国际数学竞赛】肆意多边形面积计算公式870 附和 · 46 评论文章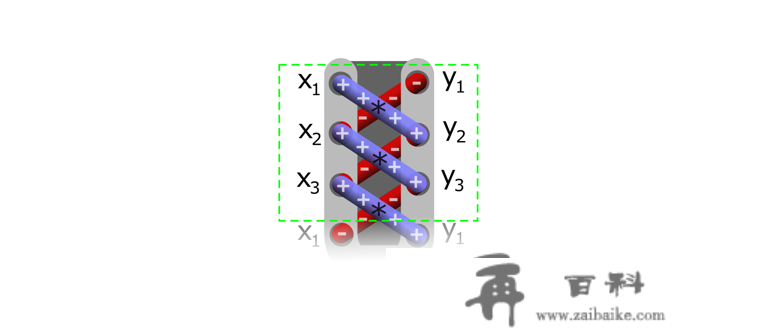
想领会更多国际数学竞赛及课程的常识,可参阅:
双木行月Tong:国际数学竞赛及课程506 附和 · 38 评论文章
