本文将推导出一些与向量和立体几何相关的三角形面积公式。
以三角形ABC的一个顶点为起点,别的两个顶点为起点,则有六个向量,我们别离求出它们的数量积:
AB→⃗⋅AC→⃗=cbcosA=cb⋅(b2+c2−a2)2bc=12(b2+c2−a2)\overrightarrow{AB} ⃗\cdot \overrightarrow{AC} ⃗=cb cosA=cb\cdot \frac{ (b^2+c^2-a^2)}{2bc}= \frac{1}{2} (b^2+c^2-a^2 )
BA→⃗⋅BC→⃗=accosB=ac⋅(a2+c2−b2)2ac=12(a2+c2−b2)\overrightarrow{BA} ⃗\cdot \overrightarrow{BC} ⃗=ac cosB=ac\cdot \frac{ (a^2+c^2-b^2)}{2ac}= \frac{1}{2} (a^2+c^2-b^2 )
CA→⃗⋅CB→⃗=abcosC=ab⋅(a2+b2−c2)2ab=12(a2+b2−c2)\overrightarrow{CA} ⃗\cdot \overrightarrow{CB} ⃗=ab cosC=ab\cdot \frac{ (a^2+b^2-c^2)}{2ab}= \frac{1}{2} (a^2+b^2-c^2 )
我们记AB→⃗⋅AC→=α\overrightarrow{AB} ⃗\cdot \overrightarrow{AC} = \alpha ,BA→⃗⋅BC→=β\overrightarrow{BA} ⃗\cdot \overrightarrow{BC} = \beta ,CA→⃗⋅CB→=γ\overrightarrow{CA} ⃗\cdot \overrightarrow{CB} = \gamma ,从以上三式中能够解出:
a2=β+αa^2 = \beta + \alpha ,b2=α+γb^2 = \alpha + \gamma ,c2=α+βc^2 = \alpha + \beta
,再代入秦九韶公式中,可得:
S△=12αβ+βγ+γαS_\triangle = \frac{1}{2} \sqrt{\alpha \beta + \beta \gamma + \gamma \alpha }
公式六十八。
公式六十九:
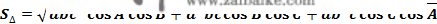
我们将两个公式分隔,就是为了提醒读者在向量运算时利用公式六十八,平面几何运算时利用公式六十九。因为向量既能够是平面向量,也能够是空间向量,所以公式六十八在空间中仍然成立。出格的,当向量以坐标形式暗示时,计算尤为简洁。
关于空间向量,《三角形的面积公式七叙》中已经给出了向量积的公式,那里,我们再给出一个用第四点指向三个顶点的向量的公式。
公式七十:

此中O为不与A、B、C重合的一点。
证明如下:

事理很简单,没必要详述,一般情况下,O城市选择坐标原点。
接下来,我们再切磋一个立体几何问题。
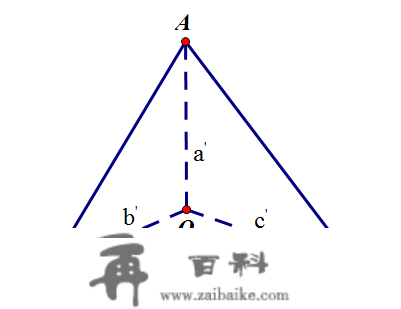
如上图所示,O-ABC是一个曲角四面体,即OA,OB,OC两两彼此垂曲,长度别离为a,b,c。h为O到面ABC的间隔,即以O为顶点,面ABC为底面的四面体的高,我们来求解一下三角形ABC的面积和高h。三角形ABC的量暗示体例稳定。
由勾股定理:a2=b′2+c′2a^2=b^2+c^2,b2=a′2+c′2b^2=a^2+c^2,c2=b′2+a′2c^2=b^2+a^2
带入秦九韶公式:S△=12a2b2−(a2+b2−c22)2S_\triangle = \frac{1}{2} \sqrt{a^2 b^2- (\frac{a^2+b^2-c^2}2)^2 }
=12(b′2+c′2)(a′2+c′2)−(b′2+c′2+a′2+c′2−b′2−a′22)2=\frac{1}{2} \sqrt{(b^{2}+c^{2} )(a^{2}+c^{2})-( \frac{b^2+c^2+a^2+c^2-b^2-a^2}{2})^2 }
=12(a′2b′2+b′2c′2+c′2a′2)= \frac{1}{2} \sqrt{(a^2 b^2+b^2 c^2+c^2 a^2 )}
记为公式七十一。
同时,我们发现:S△AOB=12a′b′S_{\triangle AOB} = \frac{1}{2} ab,S△AOC=12a′c′S_{\triangle AOC} = \frac{1}{2} ac,S△BOC=12b′c′S_{\triangle BOC} = \frac{1}{2} bc,
于是:S△AOB2+S△AOC2+S△BOC2=14(a′2b′2+b′2c′2+c′2a′2)=S△2S_{\triangle AOB}^{2} + S_{\triangle AOC}^{2} + S_{\triangle BOC}^{2} = \frac{1}{4}(a^2 b^2+b^2 c^2+c^2 a^2 ) = S_{\triangle}^{2}
即:
S△2=S△AOB2+S△AOC2+S△BOC2 S_{\triangle}^{2} =S_{\triangle AOB}^{2} + S_{\triangle AOC}^{2} + S_{\triangle BOC}^{2}
记为公式七十二。同时我们能够把此式看成立体几何的勾股定理,曲角四面体对应于曲角三角形,边长对应于面的面积,那种把线看成是面的类比,用在立体几何中,有时候会显得出格有用,我们将会在日后说到四面体时详细阐述。
将四面体的体积以面ABC为底面和以面BOC为底面,别离做体积公式,
即:VO−ABC=VA−BOCV_{O-ABC}=V_{A-BOC}
即:13⋅S△⋅h=13⋅S△BOC⋅OA\frac{1}{3}\cdot S_\triangle \cdot h= \frac{1}{3} \cdot S_{\triangle BOC}\cdot OA
即:13⋅12(a′2b′2+b′2c′2+c′2a′2)⋅h=13⋅12b′c′⋅OA\frac{1}{3}\cdot \frac{1}{2} \sqrt{(a^2 b^2+b^2 c^2+c^2 a^2 )} \cdot h= \frac{1}{3} \cdot \frac{1}{2} bc \cdot OA
于是:h=a′b′c′(a′2b′2+b′2c′2+c′2a′2)h = \frac{abc}{\sqrt{(a^2 b^2+b^2 c^2+c^2 a^2 )}}
变形能够得到:
1h2=1a′2+1b′2+1c′2\frac{1}{h^2}=\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}
总结:向量形式的公式在有关向量的问题中会显得比力有用,曲角四面体相关的面积公式能够看成是一类特殊问题的求解,它所反映出来的与平面几何中的对应关系是值得深切讨论的,记住那些类似的公式,往往能够给我们处理问题带来全新的思绪。
