本文将提出一些三角形的面积问题,并给出处理计划,并把此中的成果提炼出来做为公式利用。
已知:a+b,A-B,C,求S△S_\triangle 。
三个元素,一个长度,两个角度,求解三角形面积,足够了,事实上,那三个前提已经完全确定了一个三角形。
在求解那个问题之前,我们先导出一个叫做正切定理的公式。
a+ba−b=2RsinA+2RsinB2RsinA−2RsinB\frac{a+b}{a-b} = \frac{2R sinA + 2R sinB}{2RsinA - 2RsinB}(代入正弦定理)
=sinA+sinBsinA−SinB= \frac{sinA + sinB}{sinA - SinB}(消去2R)
=2sinA+B2cosA−B22cosA+B2sinA−B2= \frac{2 sin\frac{A+B}{2} cos\frac{A-B}{2}}{2 cos\frac{A+B}{2} sin\frac{A-B}{2}}(和差化积)
=tanA+B2tanA−B2= \frac{tan \frac{A+B}{2}}{tan \frac{A-B}{2}}
同理有:b+cb−c=tanB+C2tanB−C2\frac{b+c}{b-c} = \frac{tan \frac{B+C}{2}}{tan \frac{B-C}{2}},c+ac−a=tanC+A2tanC−A2\frac{c+a}{c-a} = \frac{tan \frac{C+A}{2}}{tan \frac{C-A}{2}}。
因为三角形内角和等于180度,所以tan(A+B2)=cotC2tan(\frac{A+B}{2}) = cot\frac{C}{2},因而正切定理也能够写成别的一个形式:a+ba−b=cotC2tanA−B2\frac{a+b}{a-b} = \frac{cot\frac{C}{2}}{tan \frac{A-B}{2}}。
以上三组式子被称为三角形的正切定理。
类似的还有正弦和余弦的式子:a+bc=cosA−B2sinC2\frac{a+b}{c} = \frac{cos \frac{A-B}{2}}{sin \frac{C}{2}},a−bc=sinA−B2cosC2\frac{a-b}{c} = \frac{sin \frac{A-B}{2}}{cos \frac{C}{2}},等等,我们不再详细推导。
下面,我们来求解之前的问题。
因为 a−b=(a+b)tanA−B2tanA+B2=(a+b)tanA−B2tanC2a-b = (a+b) \frac{tan \frac{A-B}{2}}{tan \frac{A+B}{2}} = (a+b)tan\frac{A-B}{2}tan\frac{C}{2}
再连系a+b=a+ba+b = a+b
两个式子相加,右边就能消去b,两式相减,右边就能消去a
所以:a=a+b2(1+tanA−B2tanC2)a = \frac{a+b}{2}(1 + tan\frac{A-B}{2}tan\frac{C}{2}),b=a+b2(1−tanA−B2tanC2)b= \frac{a+b}{2}(1 - tan\frac{A-B}{2}tan\frac{C}{2})
从而S△=12absinC=12(a+b)2(1−tan2A−B2tan2C2)sinCS_\triangle = \frac{1}{2}absinC = \frac{1}{2} (a+b)^2(1 - tan^2\frac{A-B}{2}tan^2\frac{C}{2})sinC
于是得到了公式七十三:
S△=12(a+b)2(1−tan2A−B2tan2C2)sinCS_{\triangle}=\frac{1}{2}(a+b)^{2}(1-tan^2\frac{A-B}{2}tan^2\frac{C}{2})sinC
置换a、b、c和A、B、C即可以得到别的两个公式。
在那个公式的推导上,我们利用了一个技巧,就是操纵了a+b=a+b,那种原来就成立,专门构建出来与要求解的式子构成一种对偶的关系式的办法是一种在求解和变形代数表达式时非常常用的,灵敏利用那种办法,关于日后解方程,求解表达式的值会显得十分便利,其根本思惟就是构建一个显而易见的式子与本来的式子构成对偶关系,然后通过等式的加减到达消元的感化。
已知:ab,a−ba+b\frac{a-b}{a+b},A-B,求S△S_\triangle 。
解:S△=12absinC=12ab2tanC21+tan2C2S_\triangle = \frac{1}{2}absinC = \frac{1}{2} ab \frac{2tan\frac{C}{2}}{1+tan^2\frac{C}{2}}(操纵三角函数的全能公式)
又由上面的正切定理:tanC2=a−ba+b1tanA−B2tan \frac{C}{2} = \frac{a-b}{a+b} \frac{1}{tan \frac{A-B}{2}},代入上式,可得:
S△=aba−ba+btanA−B2(a−ba+b)2+tan2A−B2S_\triangle = \frac{ab\frac{a-b}{a+b}tan\frac{A-B}{2}}{(\frac{a-b}{a+b})^2 + tan^2\frac{A-B}{2}}
于是有了公式七十四。置换a、b、c和A、B、C即可以得到别的两个公式。
已知:a,A,bc\frac{b}{c},求S△S_\triangle 。
解:令m=bcm=\frac{b}{c},于是b=mc,由余弦定理:a2=(mc)2+c2−2(mc)ccosAa^2 = (mc)^2 + c^2 -2(mc)ccosA,
从而c2=a2m2+1−2mcosAc^2 = \frac{a^2}{m^2 + 1 - 2mcosA},b2=a2m2m2+1−2mcosAb^2 = \frac{a^2m^2}{m^2 + 1 - 2mcosA},
将a2a^2,b2b^2,c2c^2代入秦九韶公式中,并化简,可得:
S△=12a2(bcsinA)1+(bc)2−2bccosAS_\triangle = \frac{1}{2} \frac{a^2(\frac{b}{c}sinA)}{1+(\frac{b}{c})^2-2\frac{b}{c}cosA}
于是便有下面的公式七十五。置换a、b、c和A、B、C即可以得到别的两个公式。
已知:a,A,ha2+(b+c)2=D2h_a^2 + (b+c)^2=D^2,求S△S_\triangle 。
解:由余弦定理:a2=b2+c2−2bccosA=(b+c)2−2bc(1+cosA)a^2 = b^2 + c^2-2bccosA = (b+c)^2 - 2bc(1+cosA),
所以D2=ha2+(b+c)2=(2S△a)2+a2+2bc(1+cosA)D^2 = h_a^2 + (b+c)^2 = (\frac{2S_\triangle}{a})^2 + a^2 + 2bc(1+cosA),
而S△=12bcsinAS_\triangle = \frac{1}{2}bcsinA,消去上式中的bc,可得:
S△2+4a2tanA2⋅S△+a2(a2−D2)=0S_\triangle ^2 + \frac{4a^2}{tan\frac{A}{2}}\cdot S_\triangle + a^2(a^2-D^2) = 0
那是一个关于S△S_\triangle 的一元二次方程,从中解出S△S_\triangle ,舍去负值,于是得到:
S△=a2[4+(1−D2a2)tan2A2−2]tanA2S_\triangle = \frac{a^2[\sqrt{4+(1-\frac{D^2}{a^2})tan^2\frac{A}{2}} -2]}{tan\frac{A}{2}}
于是就有公式七十六。置换a、b、c和A、B、C即可以得到别的两个公式。
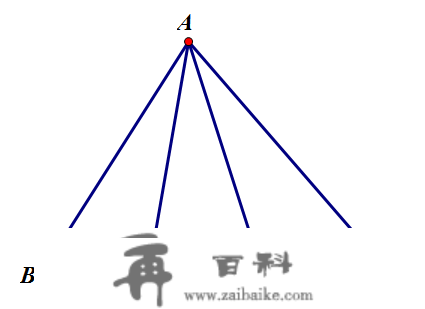
已知:如下图所示,AD、AE是三角形角A的两条三等分线,且BD=lBD=l,EC=mEC=m,求S△S_\triangle 。
解:在三角形ABD中,由正弦定理可得:b=msinA3sin(A3+C)b = \frac{m}{sin\frac{A}{3}}sin(\frac{A}{3}+C),
在三角形ACE中,由正弦定理可得:c=lsinA3sin(A3+B)c = \frac{l}{sin\frac{A}{3}}sin(\frac{A}{3}+B),
所以cb=sinCsinB=lsin(B+A3)msin(C+A3)\frac{c}{b} = \frac{sinC}{sinB} = \frac{lsin(B+\frac{A}{3})}{msin(C+\frac{A}{3})}
所以ml=sinBsin(B+A3)sinCsin(C+A3)=cosA3−cos(2B+A3)cosA3−cos(2C+A3)\frac{m}{l} = \frac{sinBsin(B+\frac{A}{3})}{sinCsin(C+\frac{A}{3})} = \frac{cos\frac{A}{3} - cos(2B+\frac{A}{3})}{cos\frac{A}{3} - cos(2C+\frac{A}{3})}
于是m−lm+l=cos(2C+A3)−cos(2B+A3)2cosA3−[cos(2B+A3)+cos(2C+A3)]=sin(B−C)sin2A3cosA3+cos2A3cos(B−C)\frac{m-l}{m+l}=\frac{cos(2C+\frac{A}{3}) - cos(2B + \frac{A}{3})}{2cos\frac{A}{3} - [cos(2B+\frac{A}{3}) + cos(2C+\frac{A}{3})]} = \frac{sin(B-C)sin\frac{2A}{3}}{cos\frac{A}{3}+cos\frac{2A}{3}cos(B-C)}
解出cos(B−C)=D(sin2A3)2−W2cosA3cos2A3(sin2A3)2+W2(cos2A3)2cos(B-C) = \frac{\sqrt{D} (sin\frac{2A}{3})^2 - W^2cos\frac{A}{3}cos\frac{2A}{3}}{(sin\frac{2A}{3})^2 + W^2(cos\frac{2A}{3})^2}
此中W=m−lm+lW = \frac{m-l}{m+l},D=sin22A3−W2sinAsinA3D = sin^2\frac{2A}{3} - W^2sinAsin\frac{A}{3}
于是S△=12bcsinA=12⋅msinA3sin(A3+C)⋅lsinA3sin(A3+B)⋅sinAS_\triangle = \frac{1}{2}bcsinA=\frac{1}{2} \cdot \frac{m}{sin\frac{A}{3}}sin(\frac{A}{3}+C) \cdot \frac{l}{sin\frac{A}{3}}sin(\frac{A}{3}+B)\cdot sinA
而sin(A3+C)⋅sin(A3+B)=12[cos(B−C)−cos(2A3+B+C)]sin(\frac{A}{3}+C) \cdot sin(\frac{A}{3}+B) = \frac{1}{2}[cos(B-C) - cos(\frac{2A}{3} +B+C)](积化和差)
因为A+B+C=πA+B+C=\pi ,所以cos(2A3+B+C)=−cosA3cos(\frac{2A}{3} +B+C) = -cos\frac{A}{3},代入面积公式,整理得:
S△=14⋅mlsinAsin2A3⋅(sin2A3D−W2cosA3cos2A3sin22A3+W2cos22A3+cosA3)S_\triangle = \frac{1}{4}\cdot \frac{mlsinA}{sin^2\frac{A}{3}}\cdot (\frac{sin\frac{2A}{3}\sqrt{D} - W^2cos\frac{A}{3}cos^2\frac{A}{3}}{sin^2\frac{2A}{3} + W^2cos^2\frac{2A}{3}} + cos\frac{A}{3})
总结:由上面的几个问题来看,求解三角形的面积,一般需要三个元素,至少有一个是边长,别的两个能够是关于角度的,也能够是关于长度的已知量。同时三角函数在运算和变更中起到了至关重要的感化,在运算中,应时刻记住三角形内角和等于180度。
