本文将给出一些利用解析几何和向量表达的三角形面积公式。我们将三角形放置在二维平面坐标系中, 并设其三点坐标为A(x1,y1)A(x_1,y_1),B(x2,y2)B(x_2,y_2),C(x3,y3)C(x_3,y_3),如下图所示:
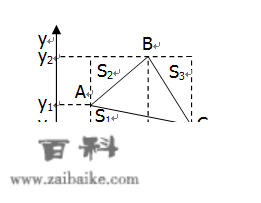
我们接纳构造已知图形面积的办法来求解未知图形面积的办法,所以我们在坐标系里对三角形ABC三个顶点做x轴和y轴的垂线,于是三角形ABC的面积能够看成是一个矩形面积减去三个四周的小三角形面积S1,S2,S3的差。
即S△=S−S1−S2−S3S_\triangle = S - S_1 - S_2 - S_3(S为虚线所示的矩形面积)
矩形面积利用底乘高,三角形面积利用底乘高的一半,可得:
S=|x3−x1|⋅|y3−y2|S = |x_3-x_1 | \cdot |y_3-y_2 |
S1=12|x3−x1|⋅|y3−y1|S_1= \frac{1}{2} |x_3-x_1 |\cdot |y_3-y_1 |
S2=12|x2−x1|⋅|y2−y1|S_2= \frac{1}{2} |x_2-x_1 |\cdot |y_2-y_1 |
S3=12|x3−x2|⋅|y3−y2|S_3= \frac{1}{2} |x_3-x_2 |\cdot |y_3-y_2 |
代入化简能够得到:
S△=12|(x2−x1)(y3−y1)−(x3−x1)(y2−y1)|S_{\triangle}=\frac{1}{2}\left| (x_{2} - x_{1})(y_{3}-y_{1})- (x_{3} - x_{1})(y_{2}-y_{1}) \right|写成二阶行列式的形式就是:
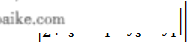
或者写成三阶行列式的形式:
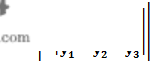
我们称之为解析公式一。
现实上解析公式一是向量积的几何意义的平面形式。空间中两个向量的向量积大小是以那两个向量为邻边的平行四边形的面积。因而空间坐标系下的三角形ABC的面积为:

我们称之为解析公式二。
上面那个向量积的公式,放到平面几何中,现实上就是《三角形的面积公式七叙》中所讨论的三角形中的线段与对边乘积的一半乘以其夹角的正弦值,因为向量积展开就是AB→×AC→=|AB|⋅|AC|sin<AB→,AC→>\vec{AB}\times \vec{AC} = |AB| \cdot |AC| sin<\vec{AB},\vec{AC}>,此中<AB→,AC→><\vec{AB},\vec{AC}>是两向量的夹角。
我们来求解下面的问题。
已知:在平面曲角坐标系中,三角形的三边所在的曲线方程别离为:l1:A1x+B1y+C1=0l_1:A_1x + B_1y + C_1 = 0,l2:A2x+B2y+C2=0l_2:A_2x + B_2y + C_2 = 0,l3:A3x+B3y+C3=0l_3:A_3x + B_3y + C_3 = 0,求三角形的面积。
那个问题看起来十分简单,只需要将三条曲线两两联立,求出它们的交点坐标,然后再操纵解析公式一就能够了,我们就照着那个思绪来求一求。
我们设A(x1,y1)A(x_1,y_1),B(x2,y2)B(x_2,y_2),C(x3,y3)C(x_3,y_3)
,为它们两两订交的交点,于是按照行列式解方程的克莱姆法例来解那个三组二元线性方程组,可得:
x1=|B1C1B2C2||A1B1A2B2|x_1 = \frac{\begin{vmatrix}B_1&C_1\\B_2&C_2\\\end{vmatrix}}{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix}},y1=|C1A1C2A2||A1B1A2B2|y_1 = \frac{\begin{vmatrix}C_1&A_1\\C_2&A_2\\\end{vmatrix}}{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix}},
x2=|B2C2B3C3||A2B2A3B3|x_2 = \frac{\begin{vmatrix}B_2&C_2\\B_3&C_3\\\end{vmatrix}}{\begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix}},y2=|C2A2C3A3||A2B2A3B3|y_2 = \frac{\begin{vmatrix}C_2&A_2\\C_3&A_3\\\end{vmatrix}}{\begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix}},
x3=|B3C3B1C1||A3B3A1B1|x_3 = \frac{\begin{vmatrix}B_3&C_3\\B_1&C_1\\\end{vmatrix}}{\begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}},y3=|C3A3C1A1||A3B3A1B1|y_3 = \frac{\begin{vmatrix}C_3&A_3\\C_1&A_1\\\end{vmatrix}}{\begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}}。
再代入解析公式一中,则有:
S△=12‖111|B1C1B2C2||A1B1A2B2||B2C2B3C3||A2B2A3B3||B3C3B1C1||A3B3A1B1||C1A1C2A2||A1B1A2B2||C2A2C3A3||A2B2A3B3||C3A3C1A1||A3B3A1B1|‖S_\triangle = \frac{1}{2}\begin{Vmatrix}1&1&1\\\frac{\begin{vmatrix}B_1&C_1\\B_2&C_2\\\end{vmatrix}}{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix}}&\frac{\begin{vmatrix}B_2&C_2\\B_3&C_3\\\end{vmatrix}}{\begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix}}&\frac{\begin{vmatrix}B_3&C_3\\B_1&C_1\\\end{vmatrix}}{\begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}}\\\frac{\begin{vmatrix}C_1&A_1\\C_2&A_2\\\end{vmatrix}}{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix}}&\frac{\begin{vmatrix}C_2&A_2\\C_3&A_3\\\end{vmatrix}}{\begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix}}&\frac{\begin{vmatrix}C_3&A_3\\C_1&A_1\\\end{vmatrix}}{\begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}}\\\end{Vmatrix}
=12⋅1|A1B1A2B2|⋅|A2B2A3B3|⋅|A3B3A1B1|⋅||A1B1A2B2||A2B2A3B3||A3B3A1B1||B1C1B2C2||B2C2B3C3||B3C3B1C1||C1A1C2A2||C2A2C3A3||C3A3C1A1||= \frac{1}{2}\cdot \frac{1}{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix} \cdot \begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix} \cdot \begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}} \cdot \begin{vmatrix}\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix}&\begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix}& \begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}\\\begin{vmatrix}B_1&C_1\\B_2&C_2\\\end{vmatrix}&\begin{vmatrix}B_2&C_2\\B_3&C_3\\\end{vmatrix}&\begin{vmatrix}B_3&C_3\\B_1&C_1\\\end{vmatrix}\\\begin{vmatrix}C_1&A_1\\C_2&A_2\\\end{vmatrix}&\begin{vmatrix}C_2&A_2\\C_3&A_3\\\end{vmatrix}&\begin{vmatrix}C_3&A_3\\C_1&A_1\\\end{vmatrix}\\\end{vmatrix}
=|12|A1B1C1A2B2C2A3B3C3|2|A1B1A2B2|⋅|A2B2A3B3|⋅|A3B3A1B1||= \left| \frac{1}{2} \frac{\begin{vmatrix}A_1&B_1&C_1\\A_2&B_2&C_2\\A_3&B_3&C_3\\\end{vmatrix}^{2} }{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix} \cdot \begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix} \cdot \begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}} \right|
我们称之为解析公式三。
我们还能够用矩阵运算的体例来推导一下解析公式三。
同样是设三条曲线的交点,即三角形的三个顶点坐标为:A(x1,y1)A(x_1,y_1),B(x2,y2)B(x_2,y_2),C(x3,y3)C(x_3,y_3),同时设
M=(A1B1C1A2B2C2A3B3C3)M = \begin{pmatrix}A_1&B_1&C_1\\A_2&B_2&C_2\\A_3&B_3&C_3\\\end{pmatrix} ,X=(x1x2x3y1y2y3111)X = \begin{pmatrix}x_1&x_2&x_3\\y_1&y_2&y_3\\1&1&1\\\end{pmatrix} ,
由解析公式一,可得S△=|12|detX||S_\triangle = |\frac{1}{2} \left| det X \right| |,即矩阵X的行列式值得一半的绝对值。
由A,B,C三点在三条曲线l1l_1,l2l_2,l3l_3上,则有:
M⋅X=diag{d1,d2,d3}M \cdot X = diag\left\{ d_1,d_2,d_3 \right\} ,此中did_i待定。
又M(x,y,1)T=(d1i,0,0)TM(x,y,1)^{T} = (d_1i, 0,0)^{T}
便有:1⋅detM=d1|A2B2A3B3|1 \cdot det M = d_1 \begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix}
于是:
d1=detM|A2B2A3B3| d_1 = \frac{det M}{\begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix}} ,同理有:d2=detM|A3B3A1B1| d_2 = \frac{det M}{\begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}} ,d3=detM|A1B1A2B2| d_3 = \frac{det M}{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix}} 。
又由M⋅X=diag{d1,d2,d3}M \cdot X = diag\left\{ d_1,d_2,d_3 \right\} ,可得:detM⋅detX=d1⋅d2⋅d3det M \cdot det X = d_1 \cdot d_2 \cdot d_3
从而S△=|12|detX||=|12|A1B1C1A2B2C2A3B3C3|2|A1B1A2B2|⋅|A2B2A3B3|⋅|A3B3A1B1||S_\triangle = |\frac{1}{2} \left| det X \right| |= \left| \frac{1}{2} \frac{\begin{vmatrix}A_1&B_1&C_1\\A_2&B_2&C_2\\A_3&B_3&C_3\\\end{vmatrix}^{2} }{\begin{vmatrix}A_1&B_1\\A_2&B_2\\\end{vmatrix} \cdot \begin{vmatrix}A_2&B_2\\A_3&B_3\\\end{vmatrix} \cdot \begin{vmatrix}A_3&B_3\\A_1&B_1\\\end{vmatrix}} \right| 。
因为我们设定了三条曲线是有三个交点的,即那三条曲线不服行,且差别时交于一个点,因而上式中的分母行列式的值就不会为0。
若是是空间中的一个三角形,三条边都是空间三维坐标系下的曲线方程,同样能够操纵类似的办法得到求解,那里就不再赘述了。
总结:关于平面解析几何入彀算三角形的面积,因为求解间隔的公式比力复杂,运算比力费事,所以凡是都是求解三点的坐标,利用解析公式一,到了空间坐标系中,才利用解析公式二,解析公式三只要在题设中的已知量情况下才会利用,不外其推导的过程和成果能够供参考。
