在高考六道解答题中，解析几何一般放在第五道的位置上。因而，不论是它的“思惟”，仍是它的“运算”，都是比力难的。
我们在处理任何一章之前，起首需要明白的是那章的常识、题型，然后才是若何运用所学的常识处理响应的题型。
起首来看测验的出题标的目的。在解析几何解答题中，第二问常考的一般有两个系列，此中以第一个系列最为常见：
1、定值最值：已知点/曲线/圆/圆锥曲线的位置关系，求各类定值和最值。
2、位置关系的断定：判断点/曲线/圆/圆锥曲线的位置关系。一、定值、最值 （一）思惟：乱用渐欲诱人眼，浅草才气没马蹄在定值最值系列，可出的题型千变万化，关于良多同窗来说老是有些纷乱复杂，也答应以用“乱用渐欲诱人眼”来描述，若是我们把要求的定值和最值（好比，证明角度是定值、证明曲线恒过定点、证明线段长度/面积为定值、计算线段长度/面积的最值等）称做“花朵”的话。
若是想更好地处理那个系列，或许我们能够做如下的拆分：
把“所求目的”当做“花朵”，把“得到点坐标的办法”当做“枝干”，然后用有限的“枝干”撑起无限万紫千红的“花朵”。
若是你要问“根”是什么？天然就是数学中的根本常识和常用思惟了。固然在一道标题问题中，它们仿佛是看不见摸不着的，但却在源源不竭地为为“枝干”和“花朵”输送着养分。所以，若是想从根源上处理解析几何那道标题问题，起首需要做的就是纯熟掌握相关的常识和数学思惟。
那里只研究“枝干”和“花朵”的部门。因为解析几何解答题中的运算较为复杂，所以一般建议先像写做文一样列出提纲。
第一部门：若何得到点坐标
第二部门：若何把待求目的翻译成点坐标“得到点坐标”的办法，一般有以下几种：
1、得到点坐标 通法：联立曲线和圆锥曲线“得到点坐标”的通用办法，一般是联立曲线和圆/圆锥曲线。
在那类标题问题中，一般是不考察曲线和圆/圆锥曲线相离的情况，而是“相切”和“订交”。
（1）“相切”的模子中，因为只要一个切点，所以只需要求出“切点坐标”即可。
圆锥曲线解答题（系列）1：联立曲线和圆锥曲线（相切） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/585809579（2）“订交”的模子中，因为有两个交点，又能够分为“两交点坐标都未知”或者“有一个点坐标已知”两种模子。
圆锥曲线解答题（系列）2：联立曲线和圆锥曲线（订交，两交点未知，设而不求） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586106704圆锥曲线解答题（系列）3：联立曲线和圆锥曲线（订交，两交点未知，都求） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586127588圆锥曲线解答题（系列）4：联立曲线和圆锥曲线（订交，一点已知一点未知） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586132019圆锥曲线解答题（系列）：联立曲线和圆锥曲线（订交，两交点已知） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586132107 特法：联立圆锥曲线和圆锥曲线若是标题问题中有“斜率”或“中点”呈现时，能够考虑“联立圆锥曲线与圆锥曲线”，也就是所谓的“（取）点（做）差法”（那种办法，仍是导数多参问题中一种模子的根底）。
圆锥曲线解答题（系列）5：联立圆锥曲线和圆锥曲线（办法操练） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586413778此中，有一些斜率相关的结论，能够间接应用于选填。若是是解答题，只需要在应用前多加一步证明即可。
圆锥曲线解答题（系列）6：联立圆锥曲线和圆锥曲线（结论记忆） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586416110 特法：间接设定需要用到的点坐标在有些标题问题中，以至不需要联立“曲线与圆/圆锥曲线”，也不需要“联立圆锥曲线与圆锥曲线”，只需要间接设定要用的点坐标即可。
圆锥曲线解答题（系列）7：间接设点 - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586418311 2、翻译目的在“翻译目的”部门，也是有良多规律能够总结的。
通法（示例：角度、曲线恒过定点、长度、面积）那里次要示范的是角度型、曲线恒过定点、长度和面积四类，其他可仿。
圆锥曲线解答题（系列）8：“赏花”篇（通法之“角度”） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/587484229圆锥曲线解答题（系列）9：“赏花”篇（通法之“曲线恒过定点”） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/587486526圆锥曲线解答题（系列）10：“赏花”篇（通法之“长度”） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/587489945圆锥曲线解答题（系列）11：“赏花”篇（通法之“面积”） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/587494011 特法：操纵几何图形及性量转换究竟结果，解析几何更侧重于“几何”，良多几何图形也有一些特定的几何性量。
若是能先把所求的目的，借助几何图形及性量转换下，就能够很好地提拔做题效率。
圆锥曲线解答题（系列）12：“赏花”篇（特法之“操纵性量转化”） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/587500583 特法：先猜后证若是所求目的仍是很难转换，则能够借助数学“先料想再证明”的思绪：斗胆地猜，小心地证。
圆锥曲线解答题（系列）13：“赏花”篇（特法之“先猜后证”） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/587502618子曰：“学而不思则罔，思而不学则殆”。通过操练提炼思惟办法，用提炼出的思惟办法处理新的标题问题。如斯频频停止，才有希望让你在看到屡见不鲜的标题问题时，有一种“浅草才气没马蹄”之感。
（二）运算：纸上得来末觉浅，绝知此事要躬行
“数学运算”做为高中数学六大核心素养（数学笼统、逻辑推理、数学建模、曲不雅想象、数据阐发和数学运算）之一，在解析几何中被表现得很充实。
固然解析几何解答题的思绪能够被提炼出来，但是详细的运算仍是需要靠本身来完成。就像陆游写的：
纸上得来末觉浅，绝知此事要躬行。在解析几何解答题中，通用的办法仍是“硬算”（好比2014年浙江理科卷的第21题，好比下面答复中联立的详细处置过程）。
圆锥曲线解答题（系列）1：联立曲线和圆锥曲线（相切） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/585809579请问那一步联立详细过程是怎么样的? - 木兰诗中有兔子的答复 - 知乎 https://www.zhihu.com/question/571153162/answer/2795494637当然，除了“硬算”之外，我们还有一些简便的办法，那里示范了此中的一些，本身也能够在日常平凡的进修中多归纳梳理。
好比，总结一些运算技巧和模子（好比，2020年北京卷的第20题，是“不合错误称构造”的通用途理办法）；
圆锥曲线解答题（系列）2：联立曲线和圆锥曲线（订交，两交点未知，设而不求） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586106704好比，记住一些常用的结论，能够极大地提拔选填的解题准确率和速度；
圆锥曲线解答题（系列）6：联立圆锥曲线和圆锥曲线（结论记忆） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586416110好比，在运算前先辈行一些转换（好比，2012年四川文科的第21题，就是把长度比转成响应的坐标比）；
圆锥曲线解答题（系列）3：联立曲线和圆锥曲线（订交，两交点未知，都求） - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/586127588好比，在列提纲时，多思虑能否有更优的解法（好比，鄙人面的例题中，供给了五种差别的解法，后两种的解题效率远远高于第一种）。
圆锥曲线解答题（系列）14：简化计算之“一题多解” - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/587504212等等等等。
但是，不管总结出的办法有几种，最末必然要靠本身多操练，才能够培育出“手感”。就像厨子解牛，“目无全牛”的前提，必然是大量的兼有效的操练。
《卖油翁》 宋 欧阳修
（原文）
陈康肃公善射，当世无双，公亦以此自矜。尝射于家圃，有卖油翁释担而立，睨之，久而不去。见其发矢十中八九，但微颔之。
康肃问曰：“汝亦知射乎？吾射不亦精乎？”翁曰：“无他，但手熟尔。”康肃忿然曰：“尔安敢轻吾射！”翁曰：“以我酌油知之。”乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿。因曰：“我亦无他，惟手熟尔。”康肃笑而遣之。
此与庄生所谓解牛、斫轮者何异？
（译文）
康肃公陈尧咨擅长射箭，世上没有第二小我能跟他相媲美，他也就凭着那种本事而自夸。曾经（有一次），（他）在家里（射箭的）场地射箭，有个卖油的老翁放下担子，站在那里斜着眼睛看着他，很久都没有分开。卖油的老头看他射十箭中了八九箭，但只是微微点点头。
陈尧咨问卖油翁：“你也懂得射箭吗？我的箭法不是很高明吗？”卖油的老翁说：“没有此外（奇妙），不外是手法纯熟罢了。”陈尧咨（听后）愤慨地说：“你怎么敢不放在眼里我射箭（的本事）！”老翁说：“凭我倒油（的经历）就能够懂得那个事理。”于是拿出一个葫芦放在地上，把一枚铜钱盖在葫芦口上，渐渐地用油杓舀油注入葫芦里，油从钱孔注入而钱却没有湿。于是说：“我也没有此外（奇妙），只不外是手纯熟罢了。”陈尧咨笑着将他送走了。
那个卖油白叟，跟庄子所说的解牛的厨子与斫轮的轮扁，有什么差别呢?（三）附加篇之“最值”：君子生非异也，善假于物也若是你去翻看高中各类试题卷，会发现选择、填空、解答题的压轴点凡是都和“取值范畴”有关。那其其实某一方面反映了数学关于现实生活的指点感化：用“起码的时间（精神或成本）”得到“最多的收成”。天然地，“最值”问题几乎能够说是数学应用的末极问题，在解析几何解答题中天然也不破例。
也正因为“最值”问题是数学中一个至关重要的问题，所以计算“最值”的思绪凡是其实不局限于解析几何的常识，而是来自于其他章节。就像我们处理解析几何的最值问题时，用到的代数常识一般来自于函数、三角函数、不等式和导数等。
也正因为如斯，我们在拆合成析几何解答题时，没必要零丁把“最值”系列提出来。我们需要做的只是，在前面搭好的积木上，再搭一块“最值”的积木即可。
圆锥曲线解答题（系列）15：附加篇~最值计算 - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/588168125
总结归纳
把上面的那些内容归纳一下吧：
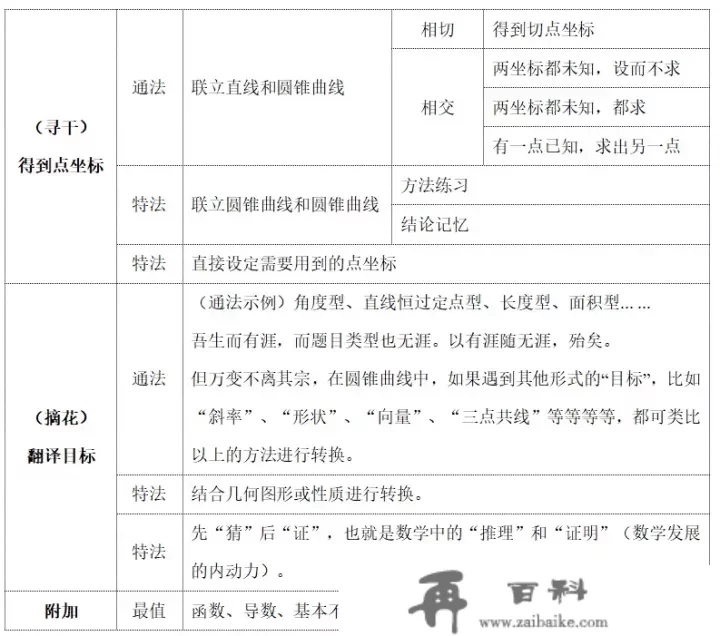二、位置关系的断定
在定值最值中，标题问题一般会告诉我们“曲线和圆锥曲线订交/相切”，然后让我们在那个根底上处置一些目的（好比，证明角度是定值、证明曲线恒过定点、证明线段长度/面积为定值、计算线段长度/面积的最值等）。
不外，在解析几何解答题中还有一类题型，只需要我们“判断出相关的位置关系”就能够。那些关系，其实不只局限于“曲线和圆锥曲线”，而是会在“点、曲线、圆、椭圆、双曲线、抛物线”中自在选择、自在组合。
不外，既然有标题问题，我们就能够试着提炼思惟和办法，进而得到一些指点性的内容，再去处理新的标题问题。
（一）点和曲线、圆、圆锥曲线的位置关系构成几何图形最根本的元素，就是“点”。
那么在解析几何中，有关“点”的位置关系的断定及应用，都有哪些常出题型呢？
解析几何解答题（系列）16：点和曲线、圆及圆锥曲线的位置关系及应用 - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/591332466 （二）曲线和曲线、圆、圆锥曲线的位置关系那个系列，是位置关系断定中最常出最重要也是最多变的模块。
解析几何解答题（系列）17：曲线和曲线、圆、椭圆、双曲线、抛物线的位置关系的断定 - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/591599272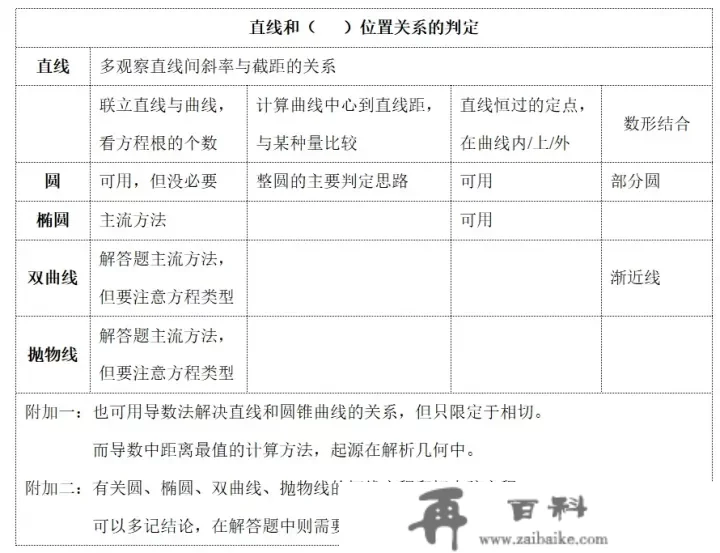
（三）圆和圆、圆锥曲线的位置关系
那么具有“完全对称性”的圆，与本身和其他圆锥曲线之间，又有哪些位置关系呢？
解析几何解答题（系列）18：圆与圆、圆锥曲线的位置关系 - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/591848675 （四）圆锥曲线之间的位置关系最初的最初，来看圆锥曲线之间的位置关系。
解析几何解答题（系列）19：圆锥曲线之间的位置关系 - 木兰诗中有兔子的文章 - 知乎 https://zhuanlan.zhihu.com/p/592130856 总结归纳总结属于你本身的系统吧。
