2009高数竞赛，小我认为实的不简单，有几道题不会，列位数学大佬可否来看看思绪是什么？

那几题很典范了，第一次做的时候也没有做出来，听教师讲最初一题其时做出来的人百里挑一。

知乎比来公式编纂换行“\\”老是出问题，能看懂就行填空题第1题

\iint_D \frac{(x+y)\ln(1+\frac{y}{x})}{\sqrt{1-x-y}}\text{d}x\text{d}y ，此中 D 是如许的一片区域

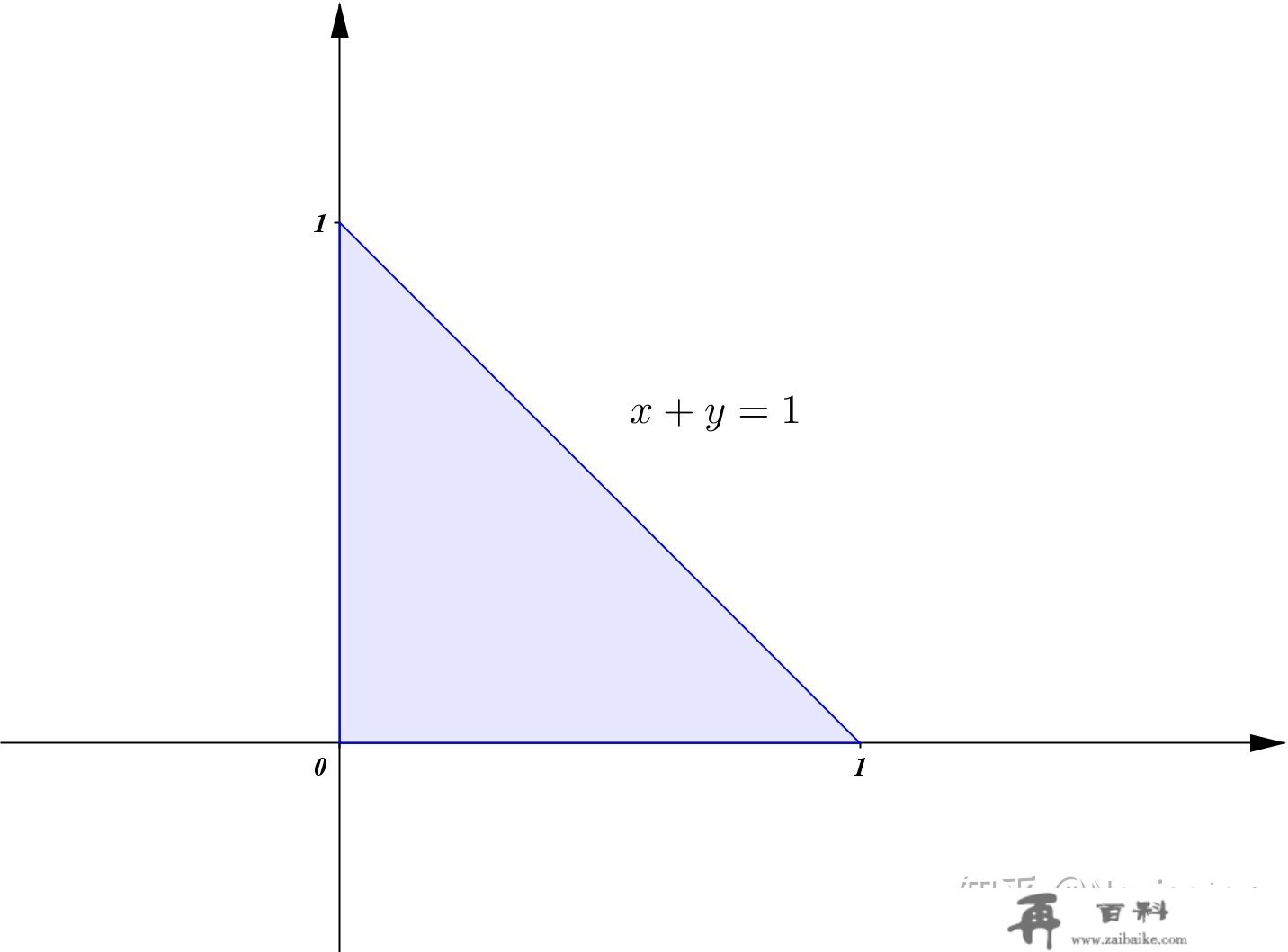
间接积分是很难的，必需要通过坐标变更，我晓得的曲角坐标换元次要有两种

（ 1 ） \begin{cases}u=x+y\\v=x\end{cases}, \begin{cases}x=v\\y=u-v\end{cases} ； （ 2 ） \begin{cases}u=x+y\\v=\frac{y}{x}\end{cases}, \begin{cases}x=\frac{u}{1+v}\\y=\frac{uv}{1+v}\end{cases}

它们的雅可比行列式别离是 |J|=\left|\left|\begin{matrix}0&1\\1&-1\end{matrix}\right|\right|=1 和 |J|=\left|\left|\begin{matrix}\frac{1}{1+v}&-\frac{u}{(1+v)^2} \\ \frac{v}{1+v}&\frac{u}{(1+v)^2}\end{matrix}\right|\right|=\frac{(1+v)^2}{u}

积分区域也能够暗示出来别离是（横u纵v）

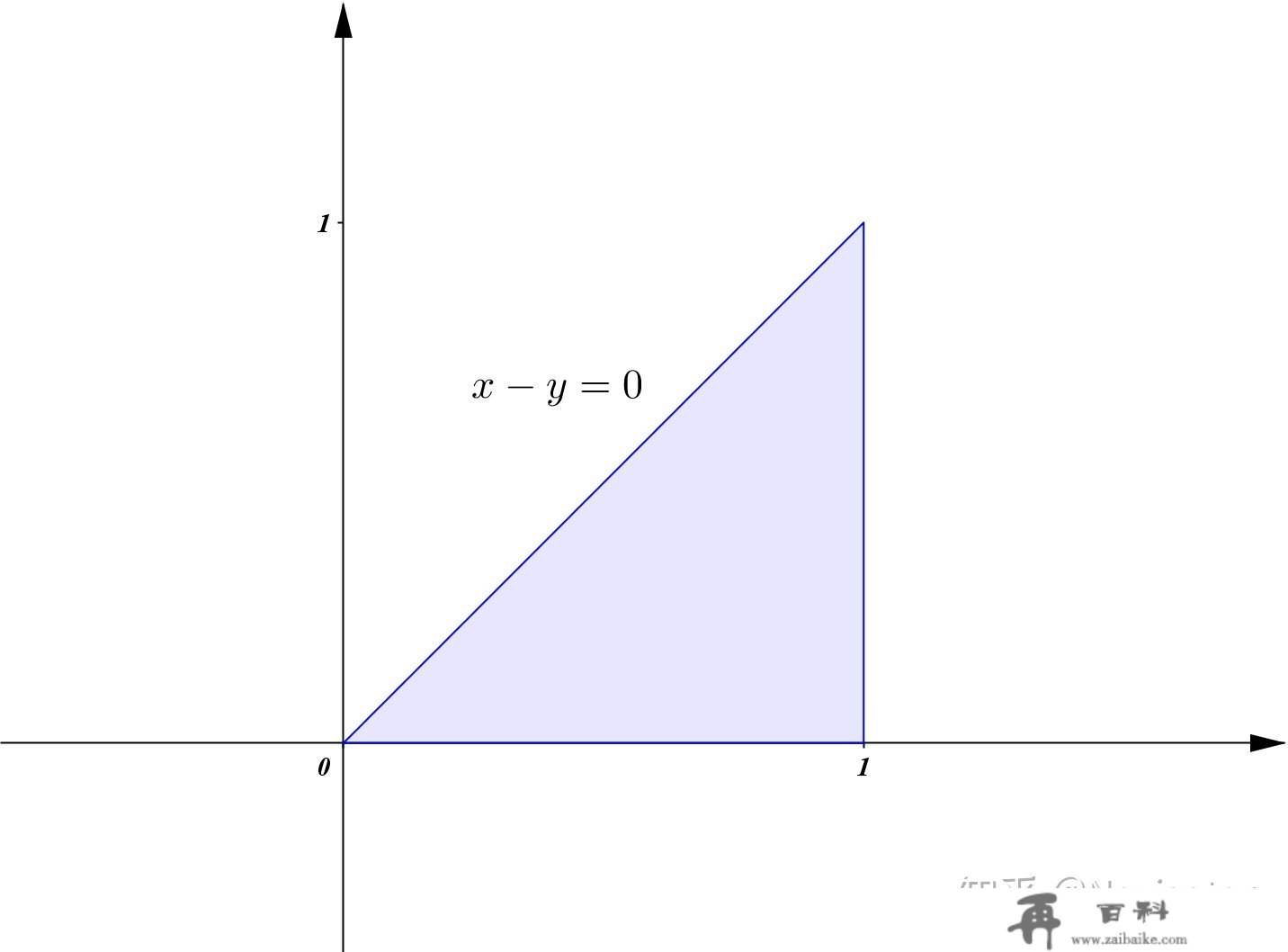
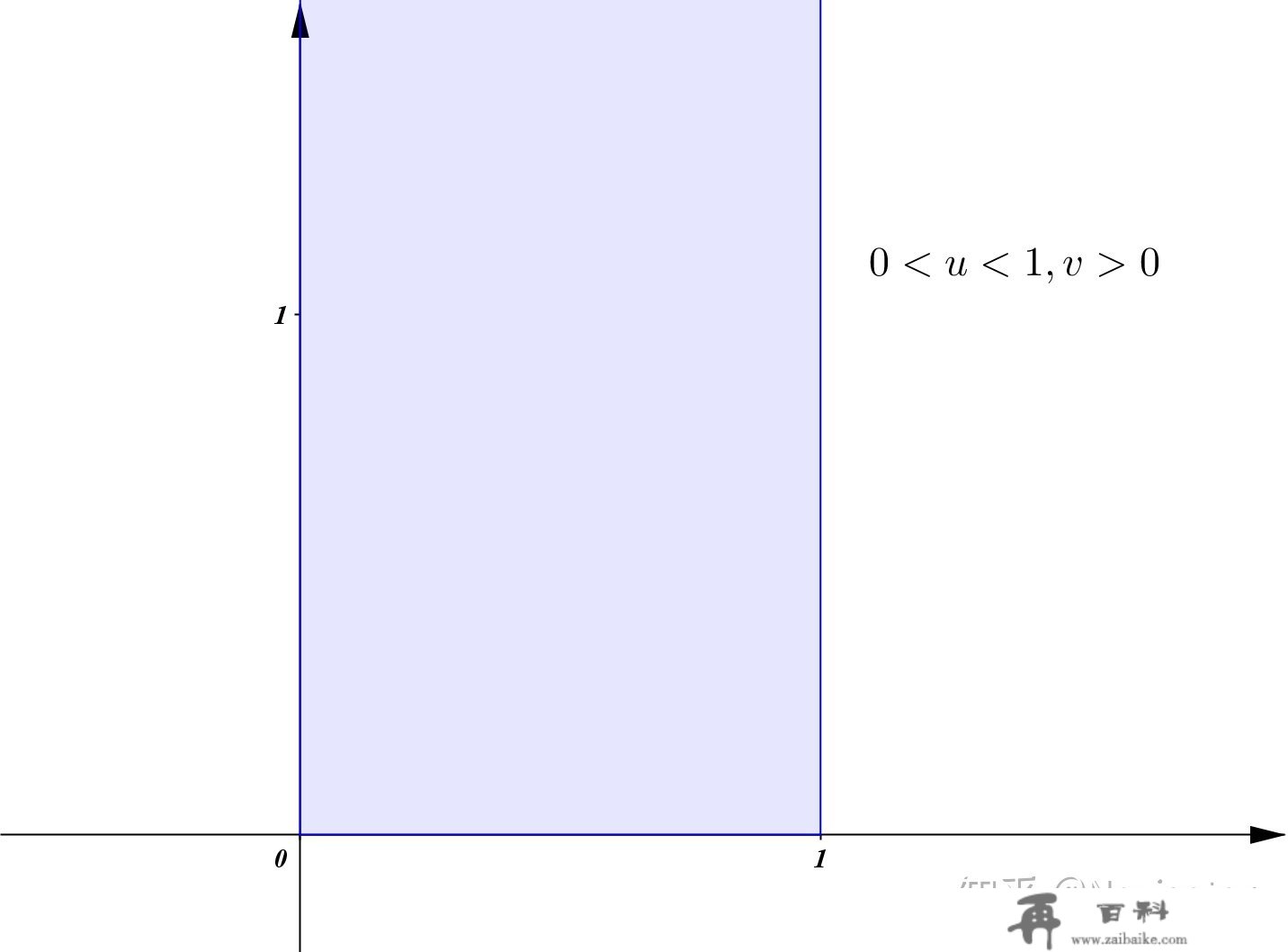
然后就能够计算了

\iint_D \frac{(x+y)\ln(1+\frac{y}{x})}{\sqrt{1-x-y}}\text{d}x\text{d}y=\int_0^1\text{d}u\int_0^u\frac{u\ln\frac{u}{v}}{\sqrt{1-u}}\text{d}v=\underbrace{\int_0^1\frac{u^2\text{d}u}{\sqrt{1-u}}}_{t=\sqrt{1-u}}=-2\int_1^0(1-t^2)^2\text{d}t=\frac{16}{15}

\iint_D \frac{(x+y)\ln(1+\frac{y}{x})}{\sqrt{1-x-y}}\text{d}x\text{d}y=\int_0^1\text{d}u\int_0^\infty \frac{u\ln(1+v)}{\sqrt{1-u}}\cdot\frac{u}{(1+v)^2}\text{d}v=\int_0^1\frac{u^2\text{d}u}{\sqrt{1-u}}\int_0^\infty \frac{\ln(1+v)}{(1+v)^2}\text{d}v

此中 \int_0^1 \underbrace{\frac{u^2\text{d}u}{ \sqrt{1-u}}}_{u=1-t^2}=2\int_0^1(1-t^2)^2=\frac{16}{15}

\int_0^\infty \frac{\ln(1+v)}{(1+v)^2}\text{d}v=- \frac{1+\ln(1+v)}{1+v}|_0^\infty=1 ，所以原式=16/15

填空题第4题

解答给出的谜底是 y=-\frac{(1-f(y))^2-f(y)}{x^2(1-f(y))^3}

题主在第三个等号那至少收了一个 y

解答题第八题