《几何画板课件造做实例教程》(微课版)绘造椭圆抛物面(z=x²/a²+y²/b²的三维曲面图形)?
媒介
几何画板其实不合适绘造三维立体图形,在外表趋向和实体外形表达都有所欠缺。若是硬要利用几何画板,也能到达目标,就是需要做图者对向量代数和空间解析几何运算有深切的领会和掌握。
下面是用GeoGebra参数绘图和操纵几何画板投影绘图的比照
 GeoGebra参照图
GeoGebra参照图 几何画板椭圆抛物面网格
几何画板椭圆抛物面网格做图步调
因为几何画板绘造立体图形,涉及空间解析几何内容较多,那里不做理论讲解和推导,仅论述做图过程。
(1)成立空间坐标系
操纵球面坐标变更公式将立体点合成到平面单元圆内。
起首设置坐标系统:显示坐标网格,选择三角坐标和方形网格,隐藏单元点。
然后在平面内绘造圆 c1c_1 ,为了做图便利,建议将圆心 OO 放在原点,半径端点 SS 落在 xx 轴。在圆上构造肆意点 Z′Z ,度量点坐标 xZ′x_{Z} 和 yZ′y_{Z} 。绘造点 A(0,yZ′)A(0,y_{Z}) 和 B(xZ′,0)B(x_{Z},0) ,毗连 Z′Z 成线段。在圆 c1c_1 上构造肆意点 X′Y′XY 。同上步调,绘造点 DD 、 CC 。

以 OO 为基点,扭转 CC 点π2\frac{π}{2} 弧度至 xx 轴得到 EE 点。
毗连点 CC 和 SS ,绘造线段 CS¯\overline{CS} 。选择线段CS¯\overline{CS} 和点 EE 构造平行线 jj ,交yy 轴于 FF 点。同样选择线段CS¯\overline{CS} 和点 DD ,构造平行线 kk ,交yy 轴于 GG 点。

依次选择点 OO 、 FF 标识表记标帜向量,选择点 DD ,平移得到点 XX ;类似操做,依次选择点 GG 、 OO 标识表记标帜向量,选择点 EE ,平移得到点 YY 。
以 OO 为基点,扭转 BB 点π2\frac{π}{2} 弧度至 yy 轴得到 ZZ 点。
那里步调繁琐,涉及的的点较多,留意操做的准确性。

构造线段 OX¯\overline{OX} 、OY¯\overline{OY}、OZ¯\overline{OZ},隐藏无关的图形要素,如许一个空间曲角坐标系就绘造完成。
(2)创建函数和构建参数
新建参数 aa , bb ;
在 c1c_1 左侧绘造两个圆 c2c_2 、 c3c_3 ,并别离在其上构建肆意点 HH 、 KK 。度量 ∠JIH∠JIH ,以及 KK 在圆 c3c_3 上点的值。

因为几何画板扭转弧度区间为[−π,π][-π,π],为了使自变量区间为 [0,2π][0,2π] ,我们新建计算 弧度t=(1−sgn(x))∗π弧度+∠JIHt=(1-sgn(x))*\pi弧度+∠JIH ;圆上点的值区间为 [0,1][0,1] ,我们放大区间,令 在上u=2∗K在c3上u=2*K在c_3上 。
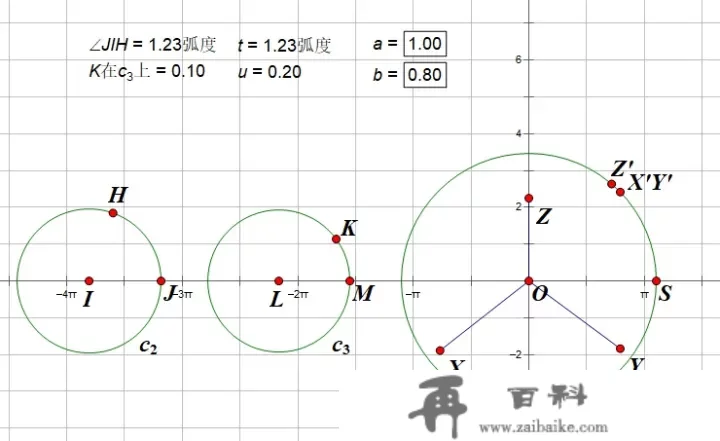
新建函数 {f(x)=a∗cos(x)∗ug(x)=b∗sin(x)∗uh(x)=u2\left\{\begin{matrix}{ f(x) =a*cos(x)*u\\ g(x)=b*sin(x)*u\\ h(x)=u^2 }\end{matrix}\right. ,新建计算 {f(t)g(t)h(t)\left\{ \begin{matrix} f(t)\\ g(t)\\ h(t) \end{matrix} \right.

(3)绘造控造点
以点 OO 位基点,别离以 、、X、Y、ZX、Y、Z 为初始点, 、、f(t)、g(t)、h(t)f(t)、g(t)、h(t) 为比值,缩放创建三个点 、、P、Q、RP、Q、R 。

选择点 QQ 、线段 OX¯\overline{OX} 创建平行线;同样选择点 PP 、线段 OY¯\overline{OY} ,创建平行线。两个平行线订交得点 TT 。

一次选择点 OO 、 RR ,标识表记标帜向量,选择点T TT ,平移得到 T1T_1 。
为了图形的美妙和整洁,我们对 T1T_1 再次平移。
在画板内画一条程度线段 P1P3¯\overline{P_1P_3} ,并在其上构造一点 P2P_2 ,选择起点 P1P_1 和中间点 P2P_2 ,标识表记标帜向量。选择 T1T_1 ,平移得到 T2T_2 。
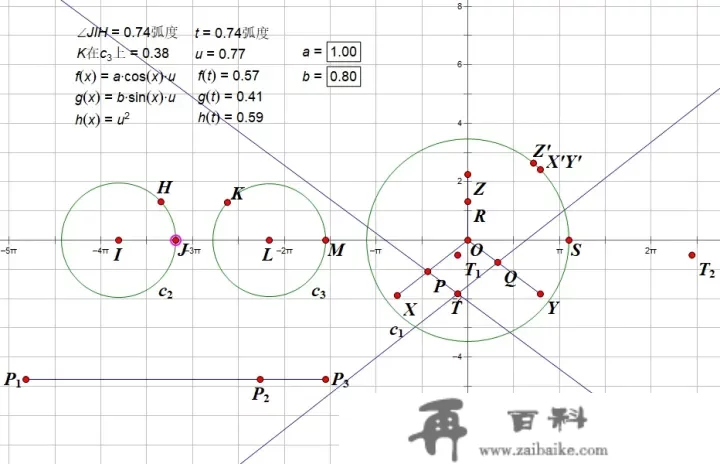
(4)构造轨迹
先绘造纬线网格。依次选择点、H、T2H、T_2 ,构造轨迹 L1L_1 。

选择点 KK 、轨迹 L1L_1 ,构造曲线族。

再绘造经线网格。依次选择点 、K、T2K、T_2 ,构造轨迹 L2L_2 。
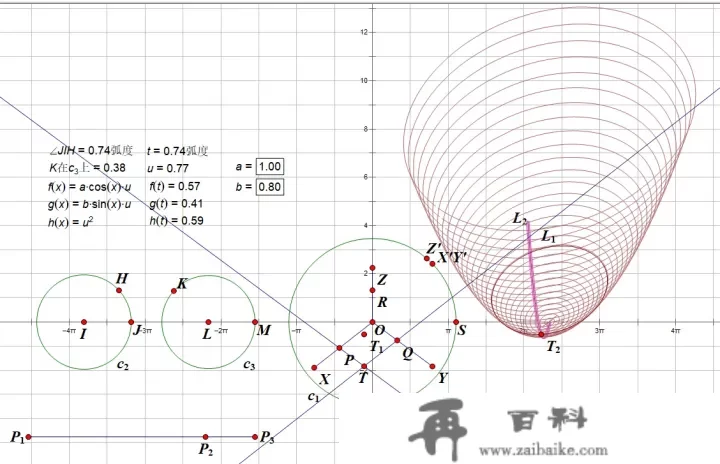
选择点HH 、轨迹L2L_2,构造曲线族。
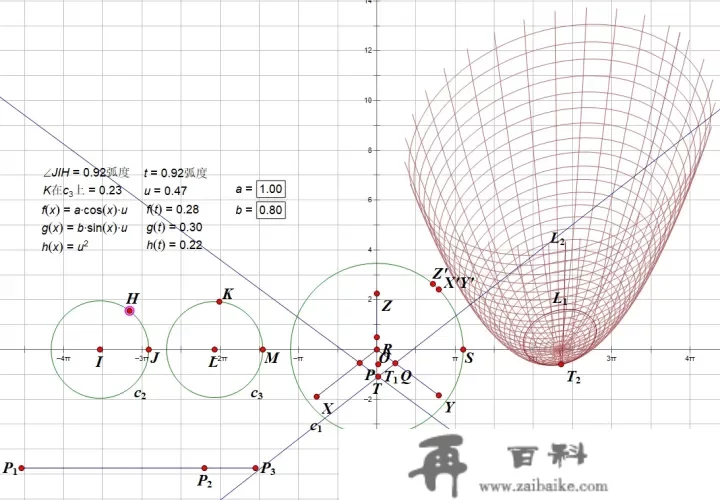
隐藏无关元素,调整空间曲角坐标系坐标系视角,最初成图。

讨论
因为不是专业绘造立体几何的软件,画板的图形采样限造,仅能显示曲面的网格骨架。
几何画板的平面应用已经长短常普遍,但是操纵其绘造立体几何和空间解析几何还需要进一步开发和摸索。
