定理1(三角形中位线定理)三角形中位线平行于第三边,而且等于第三边的一半。

如图1,DE是ΔABC的中位线,则ED∥BC,且 DE=12BCDE=\frac{1}{2}BC .
那是每一个学过初中数学的人都晓得的定理,定理证明也很容易,此处不写出证明的过程了。
从那个定理中,很容易导出一些成果,如:
(1)ΔABC的三条中位线把它划分红四个面积相等的三角形。如图1中的ΔADE,ΔBDF,ΔDFE,ΔFEC的面积相等,它们都等于 14SABC\frac{1}{4}S_{ABC} 。
(2)如图1,别离过中点D,E做平行线交BC于M,N,则平行四边形DENM的面积等于ΔABC面积的一半,即 SDENM=12SABCS_{DENM}=\frac{1}{2}S_{ABC} 。
问题是,过三角形一边的中点且平行于第三边的曲线,必然过另一边的中点吗?
谜底是必定的,不外应该证明一番。
定理2 通过ΔABC的边AB的中点的曲线与边BC平行,必通过第三边AC的中点。
阐发:画张图,如图2.点D是AB的中点,DE∥BC,要证明点E是AC的中点,也便是要证明AE=CE。

为此,我们构造平行边形:过点C做CF∥AB交DE耽误线于点F,则四边形BCFD是平行四边形,
所以CF=BD,又BD=AD,得CF=AD;
因为CF∥AB,所以∠A=∠ECF,又∠AED=∠CEF,所以ΔAED≌ΔCEF,所以AE=CE,即点E是AC的中点。
定理3 同底且位于其两侧的两个三角形ΔABC和ΔABD,若是它们面积相等,则毗连顶点的线段CD必为AB所平分。反之亦然。
阐发:画张图,如图3.已知点C、D在曲线AB两侧, SABC=SABDS_{ABC}=S_{ABD} ,要证明CD被AB平分,也便是要证明CE=DE。我们想操纵定理2来证明。
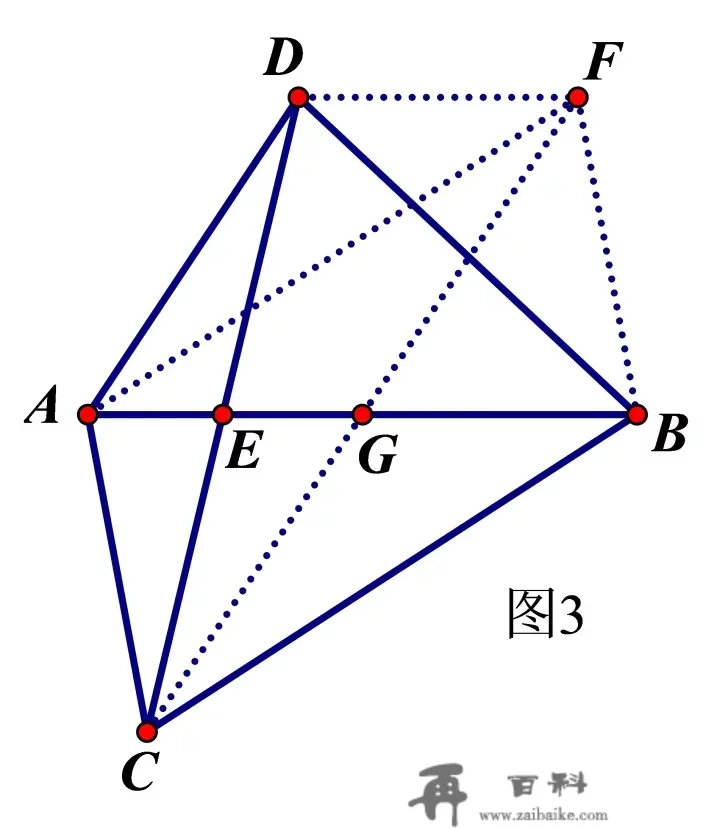
为此,我们做辅助线构造平行四边形和三角形如下:
别离做AF∥CB,BF∥CA交点为F,毗连CF,DF。毗连DF。
因为四边形ACBF是平行四边形,所以AB与CF平分,即CG=FG,且 SABC=SABFS_{ABC}=S_{ABF} ;
又因为 SABC=SABDS_{ABC}=S_{ABD} ,所以 SABF=SABDS_{ABF}=S_{ABD} ,并且ΔABD和ΔABF同底,所以它们AB边上的高相等,也便是说AB∥DF;
在ΔCDF中,因为EG∥DF,且G是CF的中点,由定理2知,E是CD的中点,即CE=DE,即CD被AB平分。
反过来能够如许论述:同底且位于其两侧的两个三角形ΔABC和ΔABD,若是毗连顶点的线段CD被AB平分,则它们面积相等。
那很好理解,如图4,别离过C,D做AB的垂线,垂中为G,F,因为CE=DE,∠CEG=∠DEF,∠CGE=∠DFE,所以ΔCGE≌ΔDEF,所以CG=DF,所以 SABC=SABDS_{ABC}=S_{ABD} 。

下面的定理结论很精致,不晓得是谁想出的。
定理4 四边形的相对边AB和CD订交于点P,设对角线AC和BD的中点为G和H,则ΔPGH的面积为四边形ABCD的面积的 14\frac{1}{4} 。
阐发:画张图,如图5.因为定理中的关键词是中点,我们也以中点做为做辅助线的起点。取AD的中点R,BC的中点Q,毗连各中位线,并耽误GQ交CP于点I,耽误RG交AP于M,耽误HQ交AP于N。
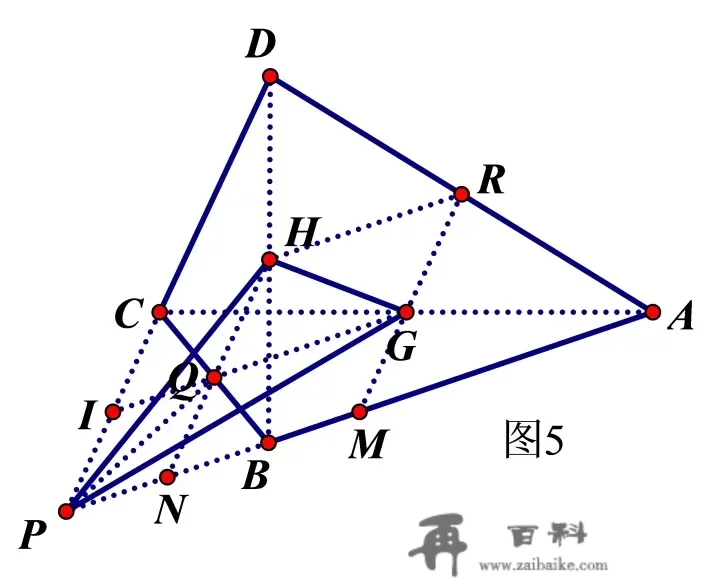
我们看到, SPGH=SPQG+SPQH+SQGHS_{PGH}=S_{PQG}+S_{PQH}+S_{QGH} ,下面别离讨论各个三角形的面积:
ΔPQG:ΔPQG与ΔCQG同底QG,且位于差别侧。因为QG∥AP,G是AC的中点,由定理2,I是CP的中点,由定理3,我们得到
SPQG=SCQG=14SABCS_{PQG}=S_{CQG}=\frac{1}{4}S_{ABC}
ΔPQH:同理,我们得到
SPQH=SBQH=14SCDBS_{PQH}=S_{BQH}=\frac{1}{4}S_{CDB}
ΔQGH:四边形QGRH是平行四边形,可见
SGQRH=SNMRH−SNMGH=12SABD−12SABCS_{GQRH}=S_{NMRH}-S_{NMGH}=\frac{1}{2}S_{ABD}-\frac{1}{2}S_{ABC}
而 SQGH=12SQGRHS_{QGH}=\frac{1}{2}S_{QGRH} ,所以
SQGH=14SABD−14SABCS_{QGH}=\frac{1}{4}S_{ABD}-\frac{1}{4}S_{ABC}
所以
SPGH=14(SABC+SCDB+SABD−SABC)=14(SCDB+SABD)=14SABCDS_{PGH}=\frac{1}{4}(S_{ABC}+S_{CDB}+S_{ABD}-S_{ABC})=\frac{1}{4}(S_{CDB}+S_{ABD})=\frac{1}{4}S_{ABCD}
定理5 三角形三条中线是共点线,共点分每条中线成2:1两条线段。
阐发:如图6.中线CD,BE必订交,设交点为O,只须证明AO的耽误线过BC的中点,也就是说,只须证明BF=CF。
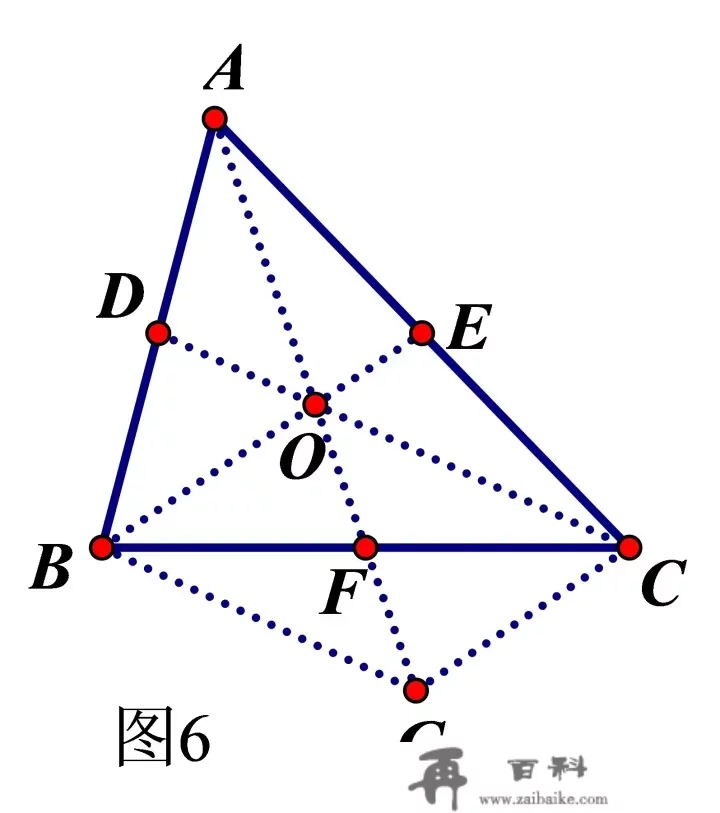
为此,我们构造平行四边形如下:
过点B做BG∥DC交AO耽误线于G,毗连GC,设AG与BC的交点为F。
因为BG∥DC,且D为AB的中点,所以点O为AG的中点;
又因为E是AC的中点,所以OE∥GC,即BO∥GC,所以四边形BGCO是平行四边形,所以BC和OG互相平分,即AF是ΔABC的中线。那就申明AF,BE,CD共线。
而AO=GO,2OF=GO,所以AO:OF=2:1.
三角形三中线的交点称为三角形的重心。
定理6(牛顿定理)完全四边形三对角线的中点共线。
如斯得到的曲线称为牛顿线。
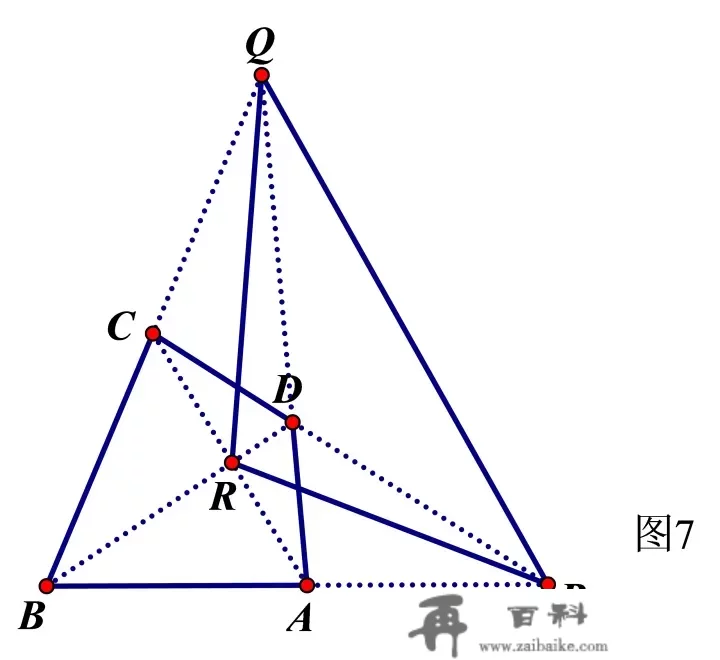
所谓完全四边形,是指平面内无三线共点的四条曲线两两订交所得到的图形。一个完全四边形有四条边和六个顶点,不在统一边上的两个顶点称为对顶点,对顶点的连线称为对角线,共有三条对角线。三对角线交成的三角形称为对角三角形。如图7,完全四边形ABCD,对角三角形为ΔPQR。
下面我们阐发定理6的证明。
阐发:如图8,完全四边形ABCD的对角线为AC,BD和PQ。取AC、BD的中点H、G,只须证明曲线颠末PQ的中点。毗连QG、QH、PG、PH,则ΔQGH和ΔPGH同底GH且位于GH的差别侧。
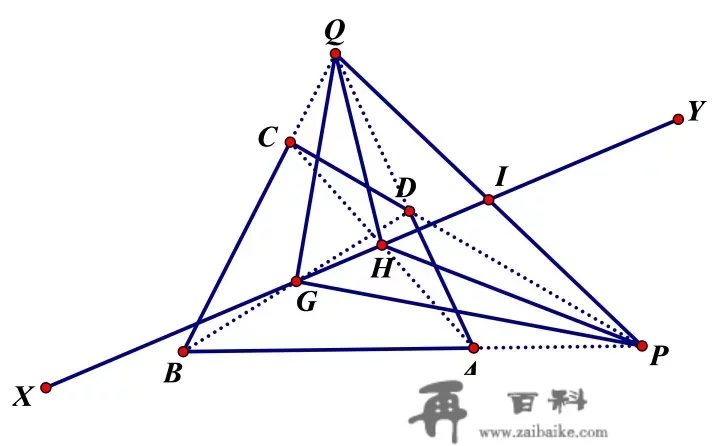
由定理4,得
SQGH=14SABCDS_{QGH}=\frac{1}{4}S_{ABCD}
SPGH=14SABCDS_{PGH}=\frac{1}{4}S_{ABCD}
所以 SQGH=SPGHS_{QGH}=S_{PGH} 。
由定理3,ΔQGH和ΔPGH顶点的连线被GH平分,或者说,曲线XY颠末PQ的中点,那是定理所需的结论。
