三角形中线的定理？

原来觉得没太多意思的一个问题，成果看到点赞更高的答复间接搬运了一些数竞平几模块比力根底的定理，还跟中线都沾不上边。大要是关于初中课内来说那些定理可能显得“高峻上”吧。还有就是平几中定理和结论太多了，困难的在于在详细的问题中识别出那一构造然后纯熟运用。

中线定义：中线是三角形中从某边的中点连向对角的顶点的线段。

由中线定义，很容易得出中线将三角形面积平分。那么关于一条线段来说，我们最关心的无非就是那条线段的长度，于是我们有：

中线长公式：三角形两边平方的和，等于所夹中线及第三边之半的平方和的两倍。

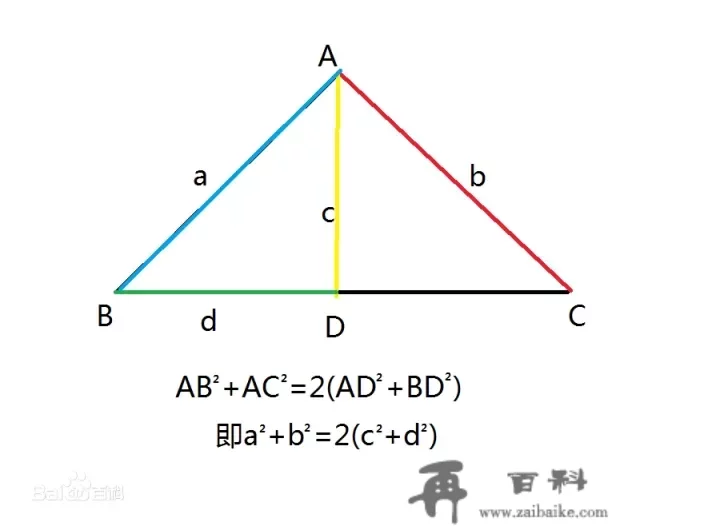中线长公式

现实上，那是斯特瓦尔特定理的一个特殊情况。

斯特瓦尔特定理：如下图所示，点 PP 在边 BCBC 上，则有 AB2⋅PC+AC2⋅BP−AP2⋅BC=BC⋅PC⋅BPAB^2\cdot PC+AC^2\cdot BP-AP^2\cdot BC=BC\cdot PC\cdot BP

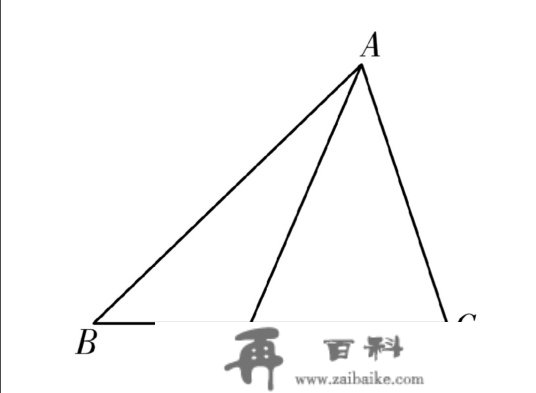斯特瓦尔特定理

那只是一条中线的性量，显然三角形有三条中线，那么我们来研究那三条中线。

三角形三条中线性量1：三条中线长的平方和等于三边长度平方和的 34\dfrac{3}{4} 。

三角形三条中线性量2：三条中线围成的三角形面积是原三角形面积的34\dfrac{3}{4}。

那两条性量证明起来比力简单，那里略去证明。那么我们还能得到如下有趣的结论：

三角形三条中线性量3：点 GG 关于点 DD 的对称点为 D1D_1 ，类似定义 E1,F1E_1,F_1 ，则有 △BGD1≅△GE1C≅△F1AG\triangle BGD_1\cong\triangle GE_1C\cong \triangle F_1AG 。

那也是显然的。

接下来，我们会发现那三角中线交于一点，该点即为重心。

重心定义：三角形三条中线的交点为重心。

重心的性量异常丰硕，而且与三角形其它特殊点搭配起来又有许多丰硕的性量，那里就只列举一些简单的性量。至于三角中线为何会共点，请自行百度塞瓦定理。

重心性量1：重心到顶点的间隔与重心到对边中点的间隔之比为 2:12:1 。

那是一条十分重要的性量，由那条性量，我们有以下间接推论：

推论1：在平面曲角坐标系中，设 △ABC\triangle ABC 三顶点坐标为 (xi,yi)(i=1,2,3)(x_i,y_i)(i=1,2,3) ，则该三角形重心坐标为 (x1+x2+x33,y1+y2+y33)\left( \dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3} \right) 。

推论2：若 GG 为三角形重心，则有 BC2+3GA2=GA2+3GB2=AB+3GC2BC^2+3GA^2=GA^2+3GB^2=AB+3GC^2 也即 GA2+GB2+GC2=13(AB2+BC2+CA2)GA^2+GB^2+GC^2=\dfrac{1}{3}(AB^2+BC^2+CA^2) 。

重心性量2：在三角形中，过重心 GG 的曲线交 AB,ACAB,AC 所在曲线别离于 P,QP,Q ，则 ABAP+ACAQ=3\dfrac{AB}{AP}+\dfrac{AC}{AQ}=3 。

重心性量3（三角形的拉格朗日定理）： GG 为 △ABC\triangle ABC 重心， PP 为平面内一点，则有 PA2+PB2+PC2=3PG2+GA2+GB2+GC2PA^2+PB^2+PC^2=3PG^2+GA^2+GB^2+GC^2 。

证明思绪：取 AGAG 中点 EE ，对 △PDE\triangle PDE 用中线长定理即得。

重心性量4：重心是三角形内到三边间隔之积更大的点。

证明思绪：设出 △ABC\triangle ABC 三边长和三角形内一点 PP 到三角形三边间隔，然后暗示出由点 PP 个三个顶点构成的三个三角形面积，利用均值不等式即可适当 PP 为重心时取等。

重心性量5：重心到三角形3个顶点间隔的平方和最小。

证明思绪：建系。

当然，既然我们给出了三角形的三条中线，那么除了数量关系以外，我们还会关心其位置关系，则有：

定理1：在 △ABC\triangle ABC 中，有两条中线 AD,BEAD,BE 和重心 GG ，则 AD⊥BEAD\bot BE 的充要前提是 AG2+BG2=CG2AG^2+BG^2=CG^2 。

最初我们略微拓展一下。

那么除了中线以外，三角形还有没有哪条特殊的线值得研究，且与中线有关呢？谜底显然是有的。

陪位中线定义：三角形一条中线关于其对应的顶点的等角线即位陪位中线。

所谓等角线，简单理解就是把中线关于那个点的角平分线做对称。

陪位中线同样也有着丰硕的性量：

陪位中线性量1：已知 △ABC\triangle ABC 与陪位中线 APAP ，则 PBPC=(ABAC)2\dfrac{PB}{PC}=\left( \dfrac{AB}{AC} \right)^2 。

陪位中线性量2：△ABC\triangle ABC的陪位中线APAP与过 B,CB,C 的三角形外接圆的切线三线共点。

当然，陪位中线是构成调和四边形的重要路子之一，但我们那里略去相关的内容。

那么，既然三条重心共点于重心，那么三条陪位中线能否共点呢？谜底是必定的：

陪位重心：三角形三条陪位中线的交点即为陪位重心。

陪位重心有时也称为类似重心。很显然，陪位重心是重心的等角共轭点（定义请自行百度）。

陪位重心性量1：三角形的陪位重心到三边间隔的平方和到达最小值。

三角形的第一莱莫恩（Lemoine）圆：过三角形陪位重心做三边的平行线与各边订交的六个交点共圆，该圆称为三角形的第一莱莫恩圆。

三角形的第二莱莫恩圆：过三角形陪位重心做各边的逆平行线与各边订交的六个交点共圆，该圆称为三角形的第二莱莫恩圆。