中点模子，望文生义，初中数学平面几何中与中点相关的几何问题。先回想一下初中数学几何中点的相关常识有哪些？
①三角形中线平分三角形面积，一般与几何图形面积连系；
②等腰三角形“三线合一”，顶角的平分线、底边的高底边中线三线合一；
③曲角三角形斜中线定理，斜边的中线等于斜边的一半；
④三角形的中位线平行且等于第三边的一半。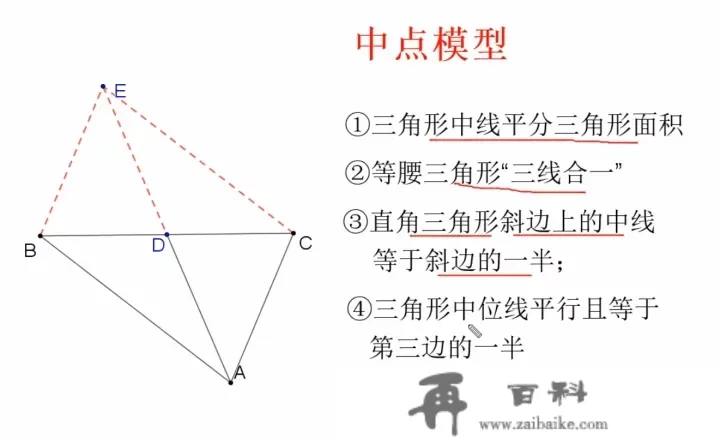
【例题】
如图，在△ABC的两边AB、AC向形外做正方形ABDE和ACFG，取BE、BC、CG的中点M、Q、N．求证：MQ＝QN。【视频讲解在文末】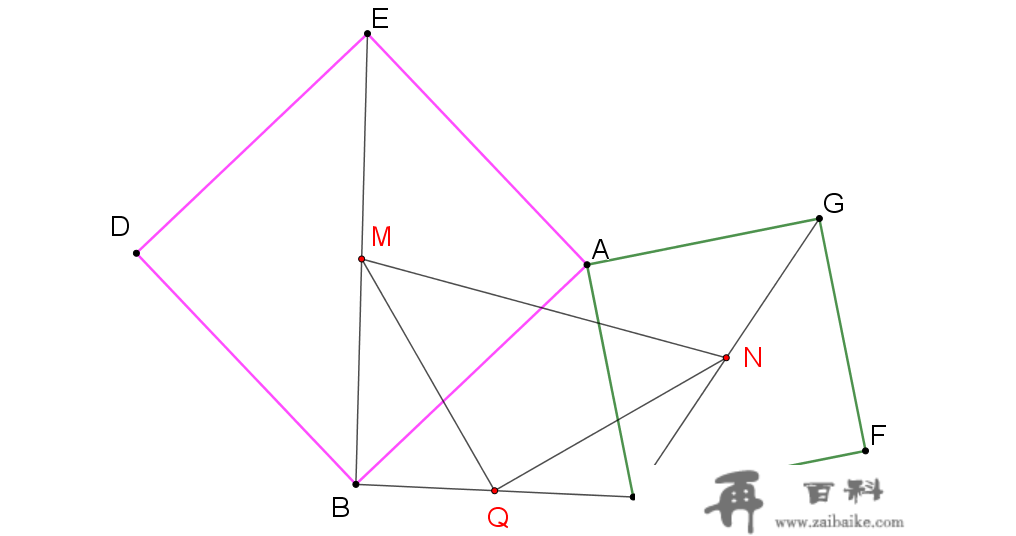
阐发：要证MQ＝QN，标题问题中点M、Q、N都是中点，中点的连线是中位线，所以那个题的打破点就在于中位线。
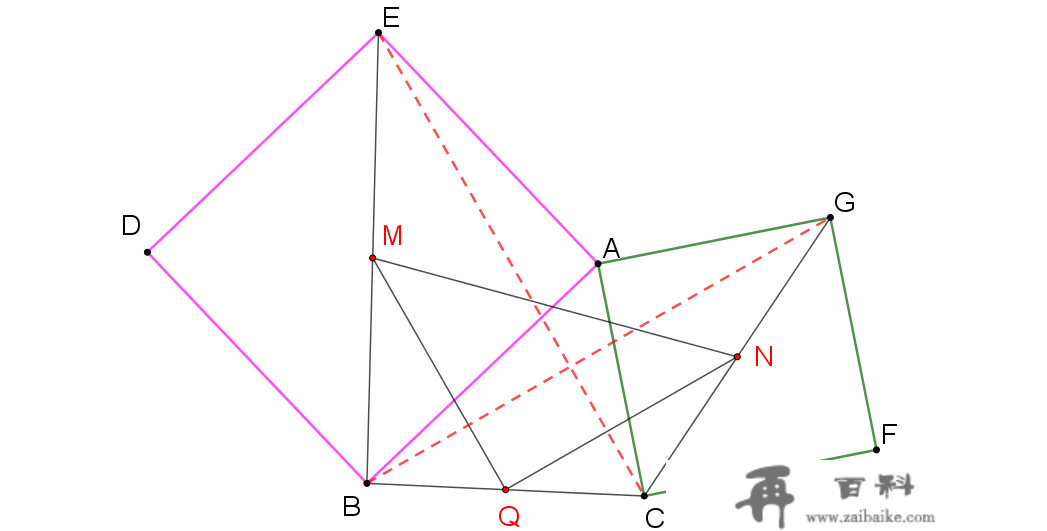
做两条辅助线，毗连EC、GB。
按照中位线的性量，能够得出：
MQ=EC/2
QN=GB/2
证MQ＝QN，就转化为证EC=GB。
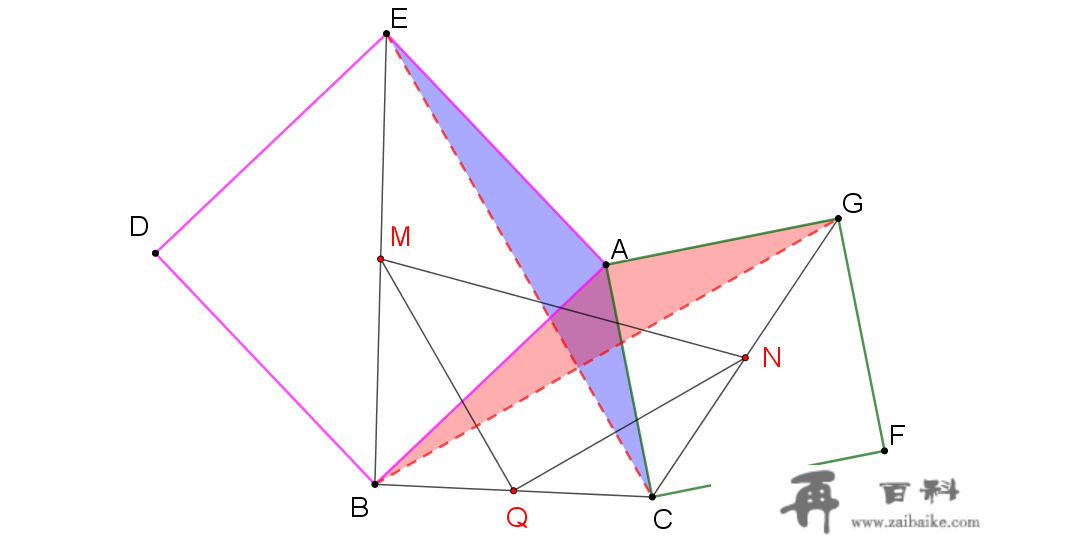
EC和GB别离是△AEC和△ABG的边，△AEC和△ABG有公共顶点A，那不就是我们之前讲过的共顶点模子吗？
初中数学G教师：初中数学：共顶点等腰曲角三角形模子例题讲解3 附和 · 0 评论文章 初中数学G教师：初中数学：共顶点模子例题讲解（2）11 附和 · 1 评论文章 初中数学G教师：初中数学：共顶点模子例题讲解（3），那个题有点难度，辅助线很关键12 附和 · 0 评论文章由正方形ABDE和正方形ACFG性量可知
AE=AB
AC=AG
∠EAB=∠GAC=90°
所以，∠EAB+∠BAC=∠GAC+∠BAC
即∠EAC=∠GAB
因而△AEC≌△ABG（SAS）
所以，就能够得出：
EC=GB，MQ＝QN。
学而思秘笈 初中数学几何辅助线专项打破+操练套拆2本
天猫
¥40.95
去购置
-视频讲解-
初中数学中点模子例题讲解（1），中点连线先找三角形的中位线！6106 播放 · 12 附和视频
0