添加辅助线是解答平面几何问题的重要手段。虽然平面几何问题变化无穷,但大大都问题都是由一些根本图形构成的,好比三角形、特殊四边形等,添加辅助线的目标就是构造那些根本图形,操纵那些根本图形的性量处理问题。
下面的例子是一个典型标题问题,很具有代表性。
如图,别离以 △ABC\triangle ABC 的AB、AC边为边长做两个正方形,毗连GD,AI垂曲于 △ABC\triangle ABC 的底边BC,耽误IA交GD于H。证明:H是GD的中点。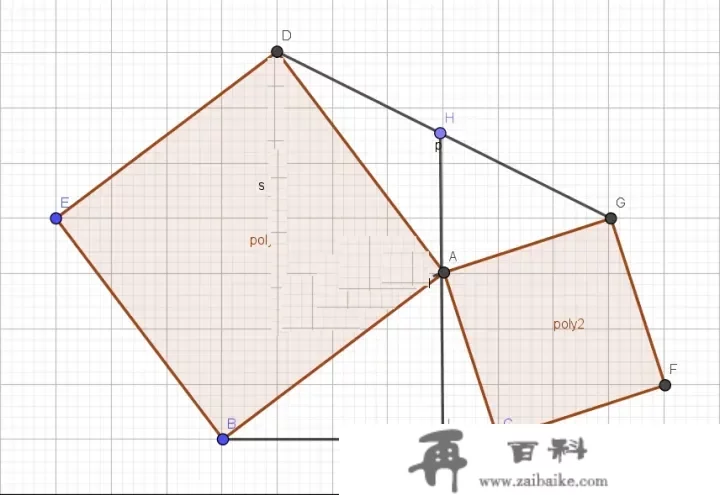
阐发:本题是典型的证明线段相等问题,思虑办法良多,好比,三角形中位线的逆定理,三角形全等,平行四边形的对角线,等等。那些都是根本图形的性量。
办法一:操纵三角形中位线的逆定理
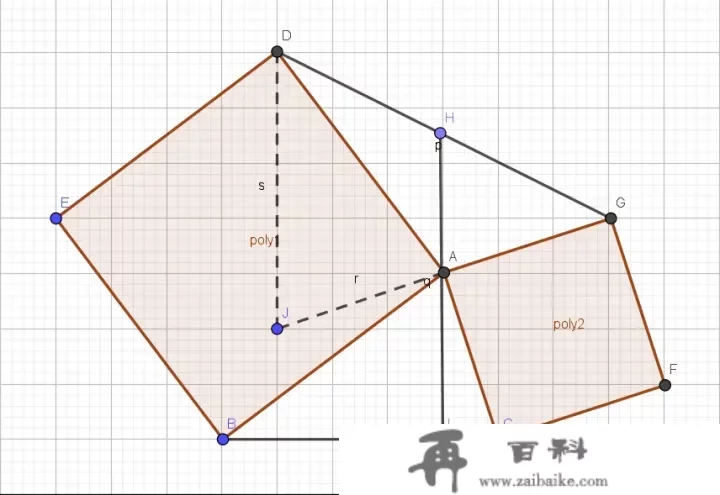
希望AH是某个三角形的中位线,标题问题中没有适宜的三角形,需要我们构造一个。
能够如许做辅助线:过D点做AH的平行线,交GA耽误线于J,希望AH是 △GDJ\triangle GDJ 的中位线,只要证明GA=AJ即可。
留意 和△ABC和△ADJ\triangle ABC 和\triangle ADJ ,那两个三角形有一边相等,再找两个角相等即可证明全等,从而AJ=AC=AG。 ∠GAH\angle GAH 和 ∠ACB\angle ACB 都是 ∠CAI\angle CAI 的余角,故相等。由辅助线平行, ∠AJD=∠GAH\angle AJD = \angle GAH ,从而 ∠AJD=∠ACB\angle AJD = \angle ACB 。同理, ∠ADJ=∠ABC\angle ADJ = \angle ABC 。所以, △ABC≅△ADJ\triangle ABC \cong \triangle ADJ ,AJ=AC=AG,AH是 △GDJ\triangle GDJ 的中位线。
办法二:操纵三角形全等

标题问题中没有适宜的三角形可用,构造两个。过G做GK垂曲AH于K,过D做DJ垂曲AH,交AH耽误线于J。留意 △AGK≅△ACI\triangle AGK \cong \triangle ACI , △ADJ≅△ABI\triangle ADJ \cong \triangle ABI ,从而,GK=AI=DJ。进而 Rt△HGK≅Rt△HDJRt\triangle HGK \cong Rt\triangle HDJ 。
办法三:操纵平行四边形的对角线。
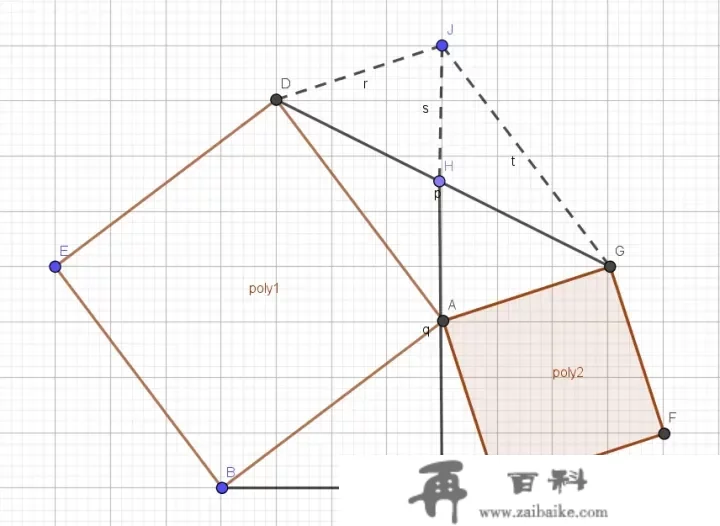
过D做DJ平行于AG,交AH耽误线于J,毗连GJ,证明DJ=AG即可。操纵 △ABC≅△ADJ\triangle ABC \cong \triangle ADJ (AD=AB, ∠ADJ=∠BAC\angle ADJ = \angle BAC , ∠DAJ=∠ABC\angle DAJ = \angle ABC ),DJ=AC=AG,得证。
