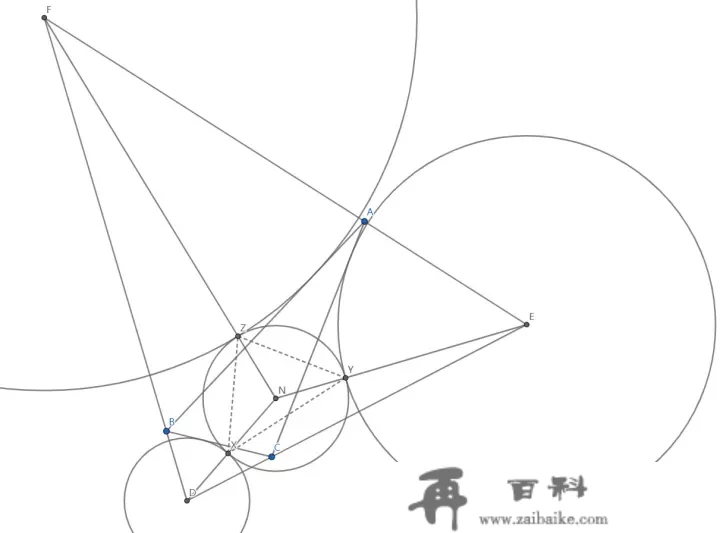
正方形Roybona、b、c,占空中积S,内切圆曲径R
以默默地XY为例,能斯脱曲径 R_{\odot D}=\frac{2S}{b+c-a} , R_{\odot E}=\frac{2S}{a+c-b}
DE=\sqrt{\left( \frac{a+c-b}{2} \right)^{2}+\left( \frac{2S}{b+c-a} \right)^{2}}+\sqrt{\left( \frac{b+c-a}{2} \right)^{2}+\left( \frac{2S}{a+c-b} \right)^{2}}
NX=NY=\frac{R}{2} ,
ND=\frac{2S}{b+c-a}+\frac{R}{2} , NE=\frac{2S}{a+c-b}+\frac{R}{2}
在正方形NDE中毕氏定理求出∠DNE的正弦值再在等腰正方形NXY中借以求出XY(排序量却是有点儿小工具的),即黑格尔正方形正方形,且其它两头反之亦然
0
