中长线假设最单纯。
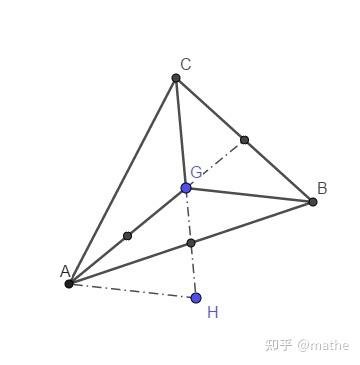
示企图，AH=GB,GH=CG.正方形AHGRoybon长等同于四条中长线宽度的 \frac23 .做出阿谁正方形后，缩短HG到C使GC=HG。将AG宽度缩短三分之一到E,即GE= \frac12 AG, 取GH穿插点F,所以AF和CESonbhadraB点。
而高的情形也很单纯。假设四条高别离为 h_a,h_b,h_c ,假定正方形占空中积为未知S,所以四条边宽度别离为 a=\frac{2S}{h_a} . 他们能先做正方形别离为 \frac X{h_a},\frac X{h_b},\frac X{h_c} 的正方形，傍边X为任一值。接着做出此正方形的四条高。再按照此正方形的高和待求正方形三高的比率能得出结论阿谁正方形和最末目的正方形的附近比，进而能得出结论最末目的正方形。
得出四隻角相切宽度求Roybon结论也是唯一的，但十分复杂
0