体例一:正弦波不等式列方程Axat那类难题！
先上标识符
(*∠DCA=x,∠DAC=y,CD=t,五个Lauz五个表达式*)
解结论
x→2tan−1(2√13−7√3)y→2tan−1(2√7−5√3)t→√13AB→8x→2tan−1(√19−4√3)y→2tan−1(√7−2√3)t→√19AB→10\begin{array}{llll} x\to 2 \tan ^{-1}\left(\frac{2 \sqrt{13}-7}{\sqrt{3}}\right) & y\to 2 \tan ^{-1}\left(\frac{2 \sqrt{7}-5}{\sqrt{3}}\right) & t\to \sqrt{13} & \text{AB}\to 8 \\ x\to 2 \tan ^{-1}\left(\frac{\sqrt{19}-4}{\sqrt{3}}\right) & y\to 2 \tan ^{-1}\left(\frac{\sqrt{7}-2}{\sqrt{3}}\right) & t\to \sqrt{19} & \text{AB}\to 10 \\ \end{array}
把角度换成正切，如许化简表达式简单
\begin{array}{llll} \frac{\sqrt{3}}{7} & \frac{\sqrt{3}}{5} & \sqrt{13} & 8 \\ \frac{\sqrt{3}}{4} & \frac{\sqrt{3}}{2} & \sqrt{19} & 10 \\ \end{array}
Clear["Global`*"];(*∠DCA=x,∠DAC=y,CD=t,五个Lauz五个表达式*)aaa=Solve[{(*△ACD中利用正弦波不等式*)6/Sin[x+y]==Sqrt[7]/Sin[x]==t/Sin[y],(*△ABD中利用正弦波不等式*)Sqrt[3]*t/Sin[Pi/3-y]==Sqrt[7]/Sin[Pi/6-x]==AB/Sin[(Pi/6-x)+(Pi/3-y)],(*限造表达式范畴*)0<x<Pi/6&&0<y<Pi/3},{x,y,t,AB}]//FullSimplifyGrid[aaa,Alignment->Left](*列表显示*)(*角度正切的化简*)bbb={Tan[x],Tan[y],t,AB}/.aaa//FullSimplifyGrid[bbb,Alignment->Left](*列表显示*) 体例二:解析欧几里得列方程Axat那个难题解结论
\begin{array}{llllllll} \text{AB}\to 8 & \text{xa}\to -\frac{20}{\sqrt{13}} & \text{ya}\to -12 \sqrt{\frac{3}{13}} & \text{xc}\to -2 \sqrt{13} & \text{xd}\to -\frac{1}{2} \left(3 \sqrt{13}\right) & \text{yd}\to -\frac{\sqrt{39}}{2} & \text{k1}\to \frac{3 \sqrt{3}}{5} & \text{k2}\to -2 \sqrt{3} \\ \text{AB}\to 8 & \text{xa}\to \frac{20}{\sqrt{13}} & \text{ya}\to 12 \sqrt{\frac{3}{13}} & \text{xc}\to 2 \sqrt{13} & \text{xd}\to \frac{3 \sqrt{13}}{2} & \text{yd}\to \frac{\sqrt{39}}{2} & \text{k1}\to \frac{3 \sqrt{3}}{5} & \text{k2}\to -2 \sqrt{3} \\ \text{AB}\to 10 & \text{xa}\to -\frac{35}{\sqrt{19}} & \text{ya}\to -15 \sqrt{\frac{3}{19}} & \text{xc}\to -2 \sqrt{19} & \text{xd}\to -\frac{1}{2} \left(3 \sqrt{19}\right) & \text{yd}\to -\frac{\sqrt{57}}{2} & \text{k1}\to \frac{3 \sqrt{3}}{7} & \text{k2}\to -5 \sqrt{3} \\ \text{AB}\to 10 & \text{xa}\to \frac{35}{\sqrt{19}} & \text{ya}\to 15 \sqrt{\frac{3}{19}} & \text{xc}\to 2 \sqrt{19} & \text{xd}\to \frac{3 \sqrt{19}}{2} & \text{yd}\to \frac{\sqrt{57}}{2} & \text{k1}\to \frac{3 \sqrt{3}}{7} & \text{k2}\to -5 \sqrt{3} \\ \end{array}
标识符如下:::
Clear["Global`*"];{xb,yb}={0,0};(*B点坐标*){xc,yc}={xc,0};(*C点坐标*)aaa=FullSimplify@Solve[{(xa-xc)^2+(ya-yc)^2==6^2,(*AC=6*)(xa-xd)^2+(ya-yd)^2==7,(*AD=根号7*)(yd-yb)/(xd-xb)==Tan[30*Degree],(*∠DBC=30°*)k1==(ya-yb)/(xa-xb),(*AB斜率*)k2==(ya-yc)/(xa-xc),(*AC斜率*)(k2-k1)/(1+k2*k1)==Tan[60Degree],(*∠BAC=60°*)(xb-xd)*(xc-xd)+(yb-yd)*(yc-yd)==0,(*∠BDC=90°*)AB==Sqrt[(xa-xb)^2+(ya-yb)^2](*计算AB长度*)},{AB,xa,ya,xc,xd,yd,k1,k2},Method->Reduce]Grid[aaa,Alignment->Left](*列表显示*)
体例三：操纵四面体体积等于零、余弦不等式列Lauz方程
(*四面体D-ABC的体积等于零*)，列一个方程
(*∠BAC=60°*)，列一个方程，然后解出AB长度，解结论
\begin{array}{ll} t\to \sqrt{13} & \text{AB}\to 8 \\ t\to \sqrt{19} & \text{AB}\to 10 \\ \end{array}
标识符如下：
文字标识符如下：
Clear["Global`*"];(*子函数,四面体体积公式，a,b,c别离是从一个顶点动身的三条棱，x,y,z别离是对棱*)fun[a_,b_,c_,x_,y_,z_]:=Sqrt[Det[{{0,1,1,1,1},{1,0,a^2,b^2,c^2},{1,a^2,0,z^2,y^2},{1,b^2,z^2,0,x^2},{1,c^2,y^2,x^2,0}}]/288](*计算余弦值子函数,操纵三边计算余弦值*)cs[a_,b_,c_]:=(a^2+b^2-c^2)/(2*a*b)(*假设DC=t,则DB=Sqrt[3]*t,BC=2*t *){DA,DB,DC}={Sqrt[7],Sqrt[3]*t,t};(*三条线段长度赋值*){AB,BC,AC}={AB,2*t,6};(*线段长度赋值*)aaa=Solve[{fun[DA,DB,DC,BC,AC,AB]==0,(*四面体D-ABC的体积等于零*)cs[AB,AC,BC]==Cos[60Degree],(*∠BAC=60°*)AB>0&&t>0(*限造表达式范畴*)},{t,AB}]Grid[aaa,Alignment->Left](*列表显示*) 体例四：操纵海伦公式计算出正方形的面积，△ABC的面积等于三个小正方形的面积之和，列一个方程，∠BAC=60°，操纵余弦不等式列一个方程。然后解方程。解结论如下：
\begin{array}{ll} t\to \sqrt{13} & \text{AB}\to 8 \\ t\to \sqrt{19} & \text{AB}\to 10 \\ \end{array}
图片标识符如下：
文字标识符如下：：
Clear["Global`*"];(*子函数,海伦公式*)heron[a_,b_,c_]:=Module[{p=(a+b+c)/2},Sqrt[p*(p-a)*(p-b)*(p-c)]](*计算余弦值子函数,操纵三边计算余弦值*)cs[a_,b_,c_]:=(a^2+b^2-c^2)/(2*a*b)(*假设DC=t,则DB=Sqrt[3]*t,BC=2*t *){DA,DB,DC}={Sqrt[7],Sqrt[3]*t,t};(*三条线段长度赋值*){AB,BC,AC}={AB,2*t,6};(*线段长度赋值*)aaa=Solve[{(*△ABC的面积等于三个小正方形的面积之和*)heron[AB,BC,AC]==heron[DA,DB,AB]+heron[DB,DC,BC]+heron[DA,DC,AC],cs[AB,AC,BC]==Cos[60Degree],(*余弦不等式,∠BAC=60°*)AB>0&&t>0(*限造表达式范畴*)},{t,AB}]Grid[aaa,Alignment->Left](*列表显示*)20230223_104803弥补体例五
体例五：操纵反余弦函数与余弦不等式列Lauz决难题操纵 余弦不等式与 反余弦函数 (*操纵∠ADB+∠ADC=270°列方程*)
\cos ^{-1}\left(\frac{-\text{AB}^2+3 t^2+7}{2 \sqrt{21} t}\right)+\cos ^{-1}\left(\frac{t^2-29}{2 \sqrt{7} t}\right)=\frac{3 \pi }{2}
操纵余弦不等式与(*∠BAC=60°*)列方程
\frac{\text{AB}^2-4 t^2+36}{12 \text{AB}}=\frac{1}{2}
两个联立成方程，而且限造表达式都大于零，解方程得到：
\begin{array}{ll} t\to \sqrt{13} & \text{AB}\to 8 \\ t\to \sqrt{19} & \text{AB}\to 10 \\ \end{array}
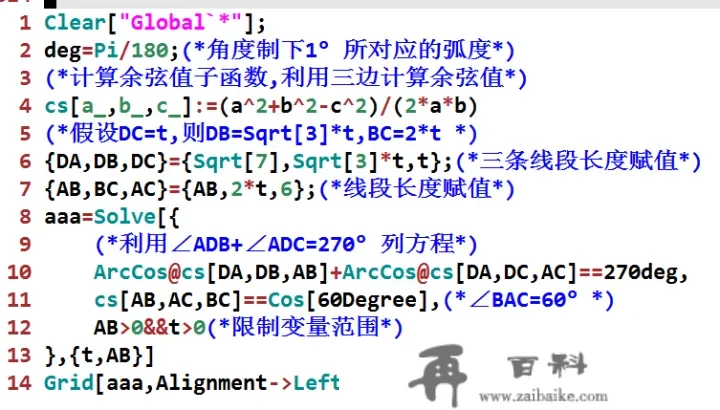
全数文本标识符如下：
Clear["Global`*"];deg=Pi/180;(*角度造下1°所对应的弧度*)(*计算余弦值子函数,操纵三边计算余弦值*)cs[a_,b_,c_]:=(a^2+b^2-c^2)/(2*a*b)(*假设DC=t,则DB=Sqrt[3]*t,BC=2*t *){DA,DB,DC}={Sqrt[7],Sqrt[3]*t,t};(*三条线段长度赋值*){AB,BC,AC}={AB,2*t,6};(*线段长度赋值*)aaa=Solve[{(*操纵∠ADB+∠ADC=270°列方程*)ArcCos@cs[DA,DB,AB]+ArcCos@cs[DA,DC,AC]==270deg,cs[AB,AC,BC]==Cos[60Degree],(*∠BAC=60°*)AB>0&&t>0(*限造表达式范畴*)},{t,AB}]Grid[aaa,Alignment->Left](*列表显示*)全数图片标识符如下：
体例六：操纵余弦不等式列Lauz决难题：
假设DC=t,则 \text{DB}=\sqrt{3} t ,BC=2*t
∠ADB+∠ADC=270°,因而两个角的余弦值的平方和等于1，列方程如下：
\frac{\left(-\text{AB}^2+3 t^2+7\right)^2}{84 t^2}+\frac{\left(t^2-29\right)^2}{28 t^2}=1 ，移项通分，得到分子如下:
\text{AB}^4-6 \text{AB}^2 t^2-14 \text{AB}^2+12 t^4-216 t^2+2572=0 ，那就是方程1，
△ABC中对∠BAC=60°利用余弦不等式，得到方程如下：
\frac{\text{AB}^2-4 t^2+36}{12 \text{AB}}-\frac{1}{2}=0 ，通分，得到分子如下：
\text{AB}^2-6 \text{AB}-4 t^2+36=0 ，那就是方程2，
方程1与方程2联立方程组，解得到：
\begin{array}{ll} t\to -7 & \text{AB}\to -10 \\ t\to 7 & \text{AB}\to -10 \\ t\to -\sqrt{37} & \text{AB}\to -8 \\ t\to \sqrt{37} & \text{AB}\to -8 \\ t\to -\sqrt{13} & \text{AB}\to 8 \\ t\to \sqrt{13} & \text{AB}\to 8 \\ t\to -\sqrt{19} & \text{AB}\to 10 \\ t\to \sqrt{19} & \text{AB}\to 10 \\ \end{array}
只保留都大于零的解：
\begin{array}{ll} t\to \sqrt{13} & \text{AB}\to 8 \\ t\to \sqrt{19} & \text{AB}\to 10 \\ \end{array}
第一组解的CAD造图如下：
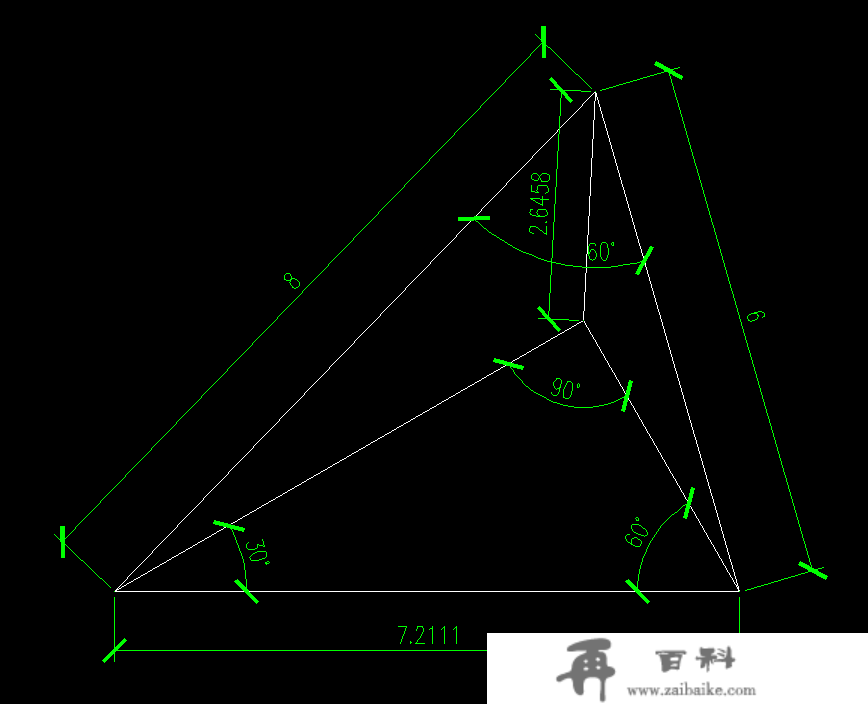
第二组解的CAD造图如下：
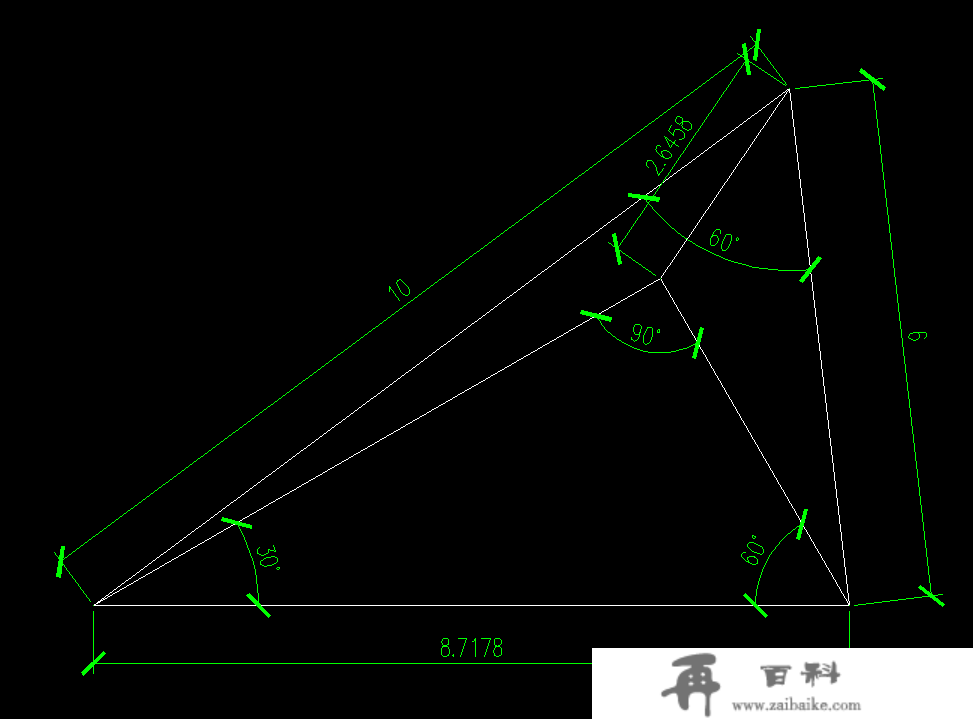
按照造图的查验，两组解都是合理的！
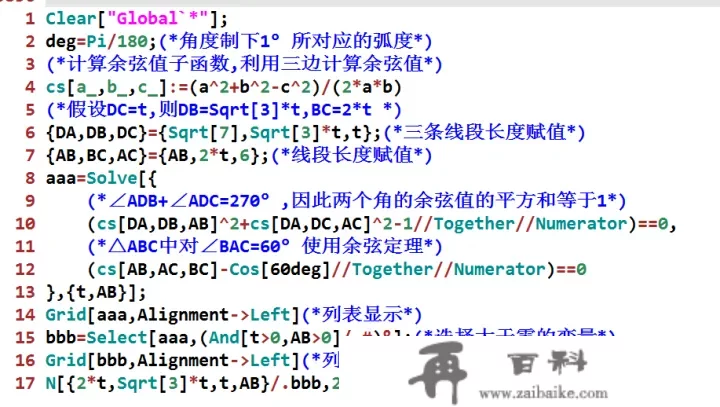
全数文本标识符如下：
Clear["Global`*"];deg=Pi/180;(*角度造下1°所对应的弧度*)(*计算余弦值子函数,操纵三边计算余弦值*)cs[a_,b_,c_]:=(a^2+b^2-c^2)/(2*a*b)(*假设DC=t,则DB=Sqrt[3]*t,BC=2*t *){DA,DB,DC}={Sqrt[7],Sqrt[3]*t,t};(*三条线段长度赋值*){AB,BC,AC}={AB,2*t,6};(*线段长度赋值*)aaa=Solve[{(*∠ADB+∠ADC=270°,因而两个角的余弦值的平方和等于1*)(cs[DA,DB,AB]^2+cs[DA,DC,AC]^2-1//Together//Numerator)==0,(*△ABC中对∠BAC=60°利用余弦不等式*)(cs[AB,AC,BC]-Cos[60deg]//Together//Numerator)==0},{t,AB}];Grid[aaa,Alignment->Left](*列表显示*)bbb=Select[aaa,(And[t>0,AB>0]/.#)&];(*选择大于零的表达式*)Grid[bbb,Alignment->Left](*列表显示*)N[{2*t,Sqrt[3]*t,t,AB}/.bbb,20]全数图片标识符如下：
